浙江省2019年高考数学模拟训练(二)
试卷更新日期:2019-03-18 类型:高考模拟
一、单选题
-
1. 已知全集 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、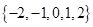 2. 双曲线 的焦点坐标是( )A、
2. 双曲线 的焦点坐标是( )A、 B、
B、 C、
C、 D、
D、 3. 复数 ( 为虚数单位)的共轭复数是( )A、
3. 复数 ( 为虚数单位)的共轭复数是( )A、 B、
B、 C、
C、 D、
D、 4. 直线 与圆 交于不同的两点 ,则 ( )A、
4. 直线 与圆 交于不同的两点 ,则 ( )A、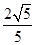 B、
B、 C、
C、 D、
5. 函数 的图像可能是( )A、
D、
5. 函数 的图像可能是( )A、 B、
B、 C、
C、 D、
D、 6. 已知平面 ,直线 满足 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 若点 位于由曲线 与 围成的封闭区域内(包括边界),则 的取值范围是( )A、
6. 已知平面 ,直线 满足 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 若点 位于由曲线 与 围成的封闭区域内(包括边界),则 的取值范围是( )A、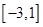 B、
B、 C、
C、 D、
D、 8. 已知四边形 中, , ,在将 沿着 翻折成三棱锥 的过程中,直线 与平面 所成角的角均小于直线 与平面 所成的角,设二面角 , 的大小分别为 ,则( )A、 B、
8. 已知四边形 中, , ,在将 沿着 翻折成三棱锥 的过程中,直线 与平面 所成角的角均小于直线 与平面 所成的角,设二面角 , 的大小分别为 ,则( )A、 B、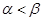 C、存在
D、
C、存在
D、 的大小关系无法确定
9. 若平面向量 满足 , , , ,则 的最大值为( )A、
的大小关系无法确定
9. 若平面向量 满足 , , , ,则 的最大值为( )A、 B、
B、 C、
C、 D、
D、 10. 设 为互不相等的三个实数,且 ,则有( )A、
10. 设 为互不相等的三个实数,且 ,则有( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 已知数列 满足 , ,则 , .
12. 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,侧视图为直角三角形,则该三棱锥的体积为 , 该三棱锥的外接球的表面积为 . 13. 在 中,角 的对边分别为 , , , ,则 , .14. 已知袋中装有大小相同质地均匀的5个球,其中3个黑球和2个白球,从袋中无放回地随机取出3个球,记取出黑球的个数为 ,则 , .15. 设 是抛物线 上相异的两点,则 的最小值是 .16. 已知函数 ,若 对任意的 恒成立,则 的取值范围是 .17. 已知集合 ,现从集合 中任意取出三个点,以这三个点为顶点能够得到个不同的直角三角形.
13. 在 中,角 的对边分别为 , , , ,则 , .14. 已知袋中装有大小相同质地均匀的5个球,其中3个黑球和2个白球,从袋中无放回地随机取出3个球,记取出黑球的个数为 ,则 , .15. 设 是抛物线 上相异的两点,则 的最小值是 .16. 已知函数 ,若 对任意的 恒成立,则 的取值范围是 .17. 已知集合 ,现从集合 中任意取出三个点,以这三个点为顶点能够得到个不同的直角三角形.三、解答题
-
18. 已知函数 .(1)、已知角 的顶点和原点 重合,始边与 轴的非负半轴重合,它的终边过点 ,求 的值;(2)、若 , ,求 的值.19. 如图,四边形 中, , , ,沿对角线 将 翻折成 ,使得 .
 (1)、证明: ;(2)、求直线 与平面 所成角的正弦值.
(1)、证明: ;(2)、求直线 与平面 所成角的正弦值.