四川省2018-2019学年高考理数一诊试卷
试卷更新日期:2019-03-18 类型:高考模拟
一、单选题
-
1. 若i是虚数单位,复数 ( )A、
 B、
B、 C、
C、 D、
D、 2. 已知命题p:“ , ”,则命题 为( )A、
2. 已知命题p:“ , ”,则命题 为( )A、 ,
,  B、
B、 ,
,  C、
C、 ,
,  D、
D、 ,
,  3. 若双曲线 的一条渐近线为 ,则实数 ( )A、2 B、4 C、6 D、84. 在 中, , , ,点D为BC边上一点,且 ,则 ( )A、
3. 若双曲线 的一条渐近线为 ,则实数 ( )A、2 B、4 C、6 D、84. 在 中, , , ,点D为BC边上一点,且 ,则 ( )A、 B、
C、1
D、2
5. 如图,某校一文化墙上的一幅圆形图案的半径为 分米,其内有一边长为 分米的正六边形的小孔,现向该圆形图案内随机地投入一飞镖(飞镖的大小忽略不计),则该飞镖落在圆形图案的正六边形小孔内的概率为( )
B、
C、1
D、2
5. 如图,某校一文化墙上的一幅圆形图案的半径为 分米,其内有一边长为 分米的正六边形的小孔,现向该圆形图案内随机地投入一飞镖(飞镖的大小忽略不计),则该飞镖落在圆形图案的正六边形小孔内的概率为( ) A、
A、 B、
B、 C、
C、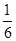 D、
D、 6. 已知函数 图象相邻两条对称轴的距离为 ,将函数 的图象向左平移 个单位后,得到的图象关于y轴对称则函数 的图象( )A、关于直线
6. 已知函数 图象相邻两条对称轴的距离为 ,将函数 的图象向左平移 个单位后,得到的图象关于y轴对称则函数 的图象( )A、关于直线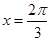 对称
B、关于直线
对称
B、关于直线  对称
C、关于点
对称
C、关于点 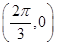 对称
D、关于点
对称
D、关于点 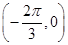 对称
7. 下列命题错误的是( )A、不在同一直线上的三点确定一个平面 B、两两相交且不共点的三条直线确定一个平面 C、如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面 D、如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面8. 的展开式中不含 项的系数的和为( )A、33 B、32 C、31 D、9. 某地环保部门召集6家企业的负责人座谈,其中甲企业有2人到会,其余5家企业各有1人到会,会上有3人发言则发言的3人来自3家不同企业的可能情况的种数为( )A、15 B、30 C、35 D、4210. 已知直线 与抛物线C: 及其准线分别交于M , N两点,F为抛物线的焦点,若 ,则m等于( )A、 B、
对称
7. 下列命题错误的是( )A、不在同一直线上的三点确定一个平面 B、两两相交且不共点的三条直线确定一个平面 C、如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面 D、如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面8. 的展开式中不含 项的系数的和为( )A、33 B、32 C、31 D、9. 某地环保部门召集6家企业的负责人座谈,其中甲企业有2人到会,其余5家企业各有1人到会,会上有3人发言则发言的3人来自3家不同企业的可能情况的种数为( )A、15 B、30 C、35 D、4210. 已知直线 与抛物线C: 及其准线分别交于M , N两点,F为抛物线的焦点,若 ,则m等于( )A、 B、 C、
C、 D、
D、 11. 已知正项等比数列 的前n项和 ,满足 ,则 的最小值为A、 B、3 C、4 D、1212. 已知函数 ,则A、0 B、1009 C、2018 D、2019
11. 已知正项等比数列 的前n项和 ,满足 ,则 的最小值为A、 B、3 C、4 D、1212. 已知函数 ,则A、0 B、1009 C、2018 D、2019二、填空题
-
13. 已知函数 ,则 .14. 已知数列 中, , ,则数列 的通项公式 .15. 九章算术 中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马” 现有一阳马,其正视图和侧视图是如图所示的直角三角形 若该阳马的顶点都在同一个球面上,且该球的表面积为 ,则该“阳马”的体积为 .
 16. 某车间租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品8件和B类产品15件,乙种设备每天能生产A类产品10件和B类产品25件,已知设备甲每天的租赁费300元,设备乙每天的租赁费400元,现车间至少要生产A类产品100件,B类产品200件,所需租赁费最少为元
16. 某车间租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品8件和B类产品15件,乙种设备每天能生产A类产品10件和B类产品25件,已知设备甲每天的租赁费300元,设备乙每天的租赁费400元,现车间至少要生产A类产品100件,B类产品200件,所需租赁费最少为元三、解答题
-
17. 在 中,内角A , B , C的对边分别为a , b , c , 若 .(1)、求A的大小;(2)、若 , ,求 的面积.18. 某大型商场在2018年国庆举办了一次抽奖活动抽奖箱里放有3个红球,3个黑球和1个白球 这些小球除颜色外大小形状完全相同 ,从中随机一次性取3个小球,每位顾客每次抽完奖后将球放回抽奖箱活动另附说明如下:
凡购物满 含 元者,凭购物打印凭条可获得一次抽奖机会;
凡购物满 含 元者,凭购物打印凭条可获得两次抽奖机会;
若取得的3个小球只有1种颜色,则该顾客中得一等奖,奖金是一个10元的红包;
若取得的3个小球有3种颜色,则该顾客中得二等奖,奖金是一个5元的红包;
若取得的3个小球只有2种颜色,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据 单位:元 ,绘制得到如图所示的茎叶图.
 (1)、求这20位顾客中获得抽奖机会的顾客的购物消费数据的中位数与平均数 结果精确到整数部分 ;(2)、记一次抽奖获得的红包奖金数 单位:元 为X , 求X的分布列及数学期望,并计算这20位顾客在抽奖中获得红包的总奖金数的平均值 假定每位获得抽奖机会的顾客都会去抽奖 .19. 如图,在棱长为2的正方体 中,M是线段AB上的动点.
(1)、求这20位顾客中获得抽奖机会的顾客的购物消费数据的中位数与平均数 结果精确到整数部分 ;(2)、记一次抽奖获得的红包奖金数 单位:元 为X , 求X的分布列及数学期望,并计算这20位顾客在抽奖中获得红包的总奖金数的平均值 假定每位获得抽奖机会的顾客都会去抽奖 .19. 如图,在棱长为2的正方体 中,M是线段AB上的动点. (1)、证明: 平面 ;(2)、若点M是AB中点,求二面角 的余弦值;(3)、判断点M到平面 的距离是否为定值?若是,求出定值;若不是,请说明理由.20. 已知椭圆C: 的离心率为 ,长轴长为4直线 与椭圆C交于A、B两点且 为直角,O为坐标原点.(1)、求椭圆C的方程;(2)、求 的最大值.
(1)、证明: 平面 ;(2)、若点M是AB中点,求二面角 的余弦值;(3)、判断点M到平面 的距离是否为定值?若是,求出定值;若不是,请说明理由.20. 已知椭圆C: 的离心率为 ,长轴长为4直线 与椭圆C交于A、B两点且 为直角,O为坐标原点.(1)、求椭圆C的方程;(2)、求 的最大值.