2017年广西柳州市、钦州市高考数学一模试卷（理科）

试卷更新日期：2017-04-26 类型：高考模拟

进入出卷网下载

一、选择题：

1. 已知集合A={x|x²﹣2x﹣3≤0}，B={y|y=2^x}，则A∩B=（）

A、（0，3] B、（0，3） C、[0，3] D、[3，+∞）

查看试题解析
2. 已知a，b∈R，i是虚数单位，若a﹣i与2+bi互为共轭复数，则（a﹣bi）²=（）

A、3+4i B、3﹣4i C、5﹣4i D、5+4i

查看试题解析
3. 甲、乙、丙三名同学6次数学测试成绩及班级平均分（单位：分）如表：
第一次
第二次
第三次
第四次
第五次
第六次
甲
95
87
92
93
87
94
乙
88
80
85
78
86
72
丙
69
63
71
71
74
74
全班
88
82
81
80
75
77
下列说法错误的是（）

A、甲同学的数学学习成绩高于班级平均水平，且较稳定 B、乙同学的数学成绩平均值是81.5 C、丙同学的数学学习成绩低于班级平均水平 D、在6次测验中，每一次成绩都是甲第一、乙第二、丙第三

查看试题解析
4. 已知平面向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} \cdot (\vec{a} + \vec{b}) = 3$ ，且 $| \vec{a} | = 2 ， | \vec{b} | = 1$ ，则向量 $\vec{a}$ 与 $\vec{b}$ 夹角的余弦值为（）

A、 $\frac{\sqrt{3}}{2}$ B、- $\frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、- $\frac{1}{2}$

查看试题解析
5. 《算法通宗》是我国古代内容丰富的数学名书，书中有如下问题：“远望巍巍塔七层，红灯向下倍加增，共灯三百八十一，请问塔顶几盏灯？”其意思为“一座塔共七层，从塔顶至塔底，每层灯的数目都是上一层的2倍，已知这座塔共有381盏灯，请问塔顶有几盏灯？”

A、3 B、4 C、5 D、6

查看试题解析
6. 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a=（）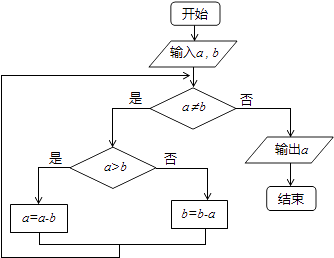

A、0 B、2 C、4 D、14

查看试题解析
7. 将函数f（x）=3sin（4x+ $\frac{π}{6}$ ）图象上所有点的横坐标伸长到原来的2倍，再向右平移 $\frac{π}{6}$ 个单位长度，得到函数y=g（x）的图象，则y=g（x）图象的一条对称轴是（）

A、x= $\frac{π}{12}$ B、x= $\frac{π}{6}$ C、 $x = \frac{π}{3}$ D、 $x = \frac{2 π}{3}$

查看试题解析
8. 在△ABC中， $B = \frac{π}{6}$ ，BC边上的高等于 $\frac{\sqrt{3}}{9} B C$ ，则cosA=（）

A、 $\frac{5 \sqrt{13}}{26}$ B、- $\frac{5 \sqrt{13}}{26}$ C、- $\frac{3 \sqrt{39}}{26}$ D、 $\frac{3 \sqrt{39}}{26}$

查看试题解析
9. 若x＞y＞1，0＜a＜b＜1，则下列各式中一定成立的是（）

A、x^a＞y^b B、x^a＜y^b C、a^x＜b^y D、a^x＞b^y

查看试题解析
10. 过双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的左焦点F作直线l与双曲线交于A，B两点，使得|AB|=4b，若这样的直线有且仅有两条，则离心率e的取值范围是（）

A、 $(1, \frac{\sqrt{5}}{2})$ B、 $(\sqrt{5}, + \infty)$ C、 $(\frac{\sqrt{5}}{2}, \sqrt{5})$ D、 $(1, \frac{\sqrt{5}}{2}) \cup (\sqrt{5}, + \infty)$

查看试题解析
11. 已知函数f（x）=|lg（x﹣1）|，若1＜a＜b且f（a）=f（b），则a+2b的取值范围为（）

A、 $(3 + 2 \sqrt{2} ， + \infty)$ B、 $[3 + 2 \sqrt{2} ， + \infty)$ C、（6，+∞） D、[6，+∞）

查看试题解析
12. 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则它的体积为（）

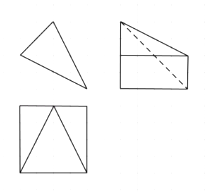A、48 B、16 C、32 D、16 $\sqrt{5}$

查看试题解析

二、填空题

13. 已知实数x，y满足条件 ${\begin{matrix} x - y \leq 0 \\ x + y \geq 0 \\ y \leq 1 \end{matrix}$ ，则z=2x+y﹣5的最小值为．

查看试题解析
14. 已知tanα=2，则 $\cos 2 α + \sin (\frac{π}{2} + α) \cos (\frac{3 π}{2} - α)$ = ．

查看试题解析
15. 已知 $a = \frac{1}{π} \int_{- 2}^{2} \sqrt{4 - x^{2}} d x$ ，则在 ${(\sqrt[3]{x} + \frac{a}{\sqrt{x}})}^{10}$ 的展开式中，所有项的系数和为．

查看试题解析
16. 已知圆C的方程为（x﹣3）²+y²=1，圆M的方程为（x﹣3﹣3cosθ）²+（y﹣3sinθ）²=1（θ∈R），过M上任意一点P作圆C的两条切线PA，PB，切点分别为A、B，则∠APB的最大值为．

查看试题解析

三、解答题

17. 设数列{a_n}的前n项和为S_n ，且λS_n=λ﹣a_n ，其中λ≠0且λ≠﹣1．

(1)、证明：{a_n}是等比数列，并求其通项公式；

(2)、若 $S_{4} = \frac{15}{16}$ ，求λ．

查看试题解析
18. 某市公租房的房源位于A，B，C，D四个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的，在该市的甲、乙、丙三位申请人中：

(1)、求恰有1人申请A片区房源的概率；

(2)、用x表示选择A片区的人数，求x的分布列和数学期望．

查看试题解析
19. 在四棱锥P﹣ABCD中， $∠ D B A = \frac{π}{2}$ ， $A B \overset{∥}{=} C D$ ，△PAB和△PBD都是边长为2的等边三角形，设P在底面ABCD的射影为O．

(1)、求证：O是AD中点；

(2)、证明：BC⊥PB；

(3)、求二面角A﹣PB﹣C的余弦值．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）经过点（2， $\sqrt{2}$ ）且离心率等于 $\frac{\sqrt{2}}{2}$ ，点A，B分别为椭圆C的左右顶点，点P在椭圆C上．

(1)、求椭圆C的方程；

(2)、M，N是椭圆C上非顶点的两点，满足OM∥AP，ON∥BP，求证：三角形MON的面积是定值．

查看试题解析
21. 已知函数f（x）=x²+2x+alnx（a∈R）．

(1)、讨论函数f（x）的单调性；

(2)、当t≥1时，不等式f（2t﹣1）≥2f（t）﹣3恒成立，求实数a的取值范围．

查看试题解析
22. 已知曲线C在直角坐标系xOy下的参数方程为 ${\begin{matrix} x = 1 + \sqrt{3} \cos θ \\ y = \sqrt{3} \sin θ \end{matrix}$ （θ为参数）．以O为极点，x轴的非负半轴为极轴建立极坐标系．

(1)、求曲线C的极坐标方程；

(2)、直线l的极坐标方程是ρcos（θ﹣ $\frac{π}{6}$ ）=3 $\sqrt{3}$ ，射线OT：θ= $\frac{π}{3}$ （ρ＞0）与曲线C交于A点，与直线l交于B，求线段AB的长．

查看试题解析
23. 已知关于x的不等式|x﹣2|﹣|x+3|≥|m+1|有解，记实数m的最大值为M．

(1)、求M的值；

(2)、正数a，b，c满足a+2b+c=M，求证： $\frac{1}{a + b}$ + $\frac{1}{b + c}$ ≥1．

查看试题解析

	第一次	第二次	第三次	第四次	第五次	第六次
甲	95	87	92	93	87	94
乙	88	80	85	78	86	72
丙	69	63	71	71	74	74
全班	88	82	81	80	75	77