2017年浙江省杭州市萧山区瓜沥片中考数学模拟试卷（3月份）

试卷更新日期：2017-04-26 类型：中考模拟

进入出卷网下载

一、仔细选一选

1. $\sqrt{16}$ 的值等于（）

A、4 B、﹣4 C、±2 D、2

查看试题解析
2. 如果ax²+2x+ $\frac{1}{2}$ =（2x+ $\frac{1}{2}$ ）²+m，则a，m的值分别是（）

A、2，0 B、4，0 C、2， $\frac{1}{4}$ D、4， $\frac{1}{4}$

查看试题解析
3. 已知二次函数y=ax²+bx+c的图象如图所示，则下列6个代数式：ab、ac、a+b+c、2a+b、2a﹣b中，其值为正的式子的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 如图，身高为1.5米的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3米，CA=1米，则树的高度为（）

A、3米 B、4米 C、4.5米 D、6米

查看试题解析
5. 多多班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，下列说法正确的是（）

A、极差是47 B、众数是42 C、中位数是58 D、每月阅读数量超过40的有4个月

查看试题解析
6. 如图，在Rt△ABC内有边长分别为a，b，c的三个正方形，则a，b，c满足的关系式是（）

A、b=a+c B、b=ac C、b²=a²+c² D、b=2a=2c

查看试题解析
7. 小兰画了一个函数y= $\frac{a}{x} - 1$ 的图象如图，那么关于x的分式方程 $\frac{a}{x} - 1$ =2的解是（）

A、x=1 B、x=2 C、x=3 D、x=4

查看试题解析
8. 如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于点E，且DE∥BC．已知AE=2 $\sqrt{2}$ ，AC=3 $\sqrt{2}$ ，BC=6，则⊙O的半径是（）

A、3 B、4 C、4 $\sqrt{3}$ D、2 $\sqrt{3}$

查看试题解析
9. 如图，OA⊥OB，等腰直角三角形CDE的腰CD在OB上，∠ECD=45°，将三角形CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则 $\frac{O C}{C D}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
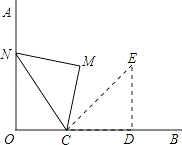10. 以下说法：
①关于x的方程x+ $\frac{1}{x}$ =c+ $\frac{1}{c}$ 的解是x=c（c≠0）；
②方程组 ${\begin{matrix} x y + y z = 63 \\ x z + y z = 23 \end{matrix}$ 的正整数解有2组；
③已知关于x，y的方程组 ${\begin{matrix} x + 3 y = 4 - a \\ x - y = 3 a \end{matrix}$ ，其中﹣3≤a≤1，当a=1时，方程组的解也是方程x+y=4﹣a的解；
其中正确的有（）

A、②③ B、①② C、①③ D、①②③

查看试题解析

二、认真填一填

11. 已知无理数1+2 $\sqrt{3}$ ，若a＜1+2 $\sqrt{3}$ ＜b，其中a、b为两个连续的整数，则ab的值为．

查看试题解析
12. 若一组数据 1，2，3，x的平均数是2，则这组数据的方差是．

查看试题解析
13. 如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E，CD=4 $\sqrt{2}$ ，AE=2，则⊙O的半径为．

查看试题解析
14. 一个几何体，是由许多规格相同的小正方体堆积而成的，其主视图，左视图如图所示要摆成这样的图形，至少需用块小正方体．

查看试题解析
15. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，则 $\frac{b}{a}$ 的值为； $\frac{c}{a}$ 的取值范围为．

查看试题解析
16.
已知，如图，双曲线y= $\frac{4}{x}$ （x＞0）与直线EF交于点A，点B，且AE=AB=BF，连结AO，BO，它们分别与双曲线y= $\frac{2}{x}$ （x＞0）交于点C，点D，则：

(1)、①AB与CD的位置关系是；
②四边形ABDC的面积为．

查看试题解析

三、全面答一答

17.
请用直尺和圆规在所给的两个矩形中各作一个不为正方形的菱形，且菱形的四个顶点都在矩形的边上，面积相同的图形视为同一种．（保留作图痕迹）．

查看试题解析
18. 先化简，再求代数式的值：（ $\frac{2}{a - 1}$ ﹣ $\frac{a + 2}{a^{2} - 1}$ ）÷ $\frac{a}{a - 1}$ ，其中sin²30°＜a＜tan²60°，请你取一个合适的整数作为a的值代入求值．

查看试题解析
19. 在一个不透明的盒子里，装有四个分别标有数字﹣1，﹣2，﹣3，﹣4的小球，它们的形状、大小、质地等完全相同．小强先从盒子里随机取出一个小球，记下数字为x；放回盒子摇匀后，再由小华随机取出一个小球，记下数字为y．

(1)、用列表法或画树状图表示出（x，y）的所有可能出现的结果；

(2)、求小强、小华各取一次小球所确定的点（x，y）落在一次函数y=x﹣1图象上的概率．

查看试题解析
20.
如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（4，2）．过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N．

(1)、求过O，B，E三点的二次函数关系式；

(2)、求直线DE的解析式和点M的坐标；

(3)、若反比例函数y= $\frac{m}{x}$ （x＞0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上．

查看试题解析
21.
如图，在平行四边形ABCD中，E为BC边上的一点，且AE与DE分别平分∠BAD和∠ADC

(1)、求证：AE⊥DE；

(2)、设以AD为直径的半圆交AB于F，连结DF交AE于G，已知CD=5，AE=8．

①求BC的长；
②求 $\frac{F G}{A F}$ 值．

查看试题解析
22.
如图1，在矩形ABCD中，AB=4，AD=2，点P是边AB上的一个动点（不与点A、点B重合），点Q在边AD上，将△CBP和△QAP分别沿PC、PQ折叠，使B点与E点重合，A点与F点重合，且P、E、F三点共线．

(1)、若点E平分线段PF，则此时AQ的长为多少？

(2)、若线段CE与线段QF所在的平行直线之间的距离为2，则此时AP的长为多少？

(3)、在“线段CE”、“线段QF”、“点A”这三者中，是否存在两个在同一条直线上的情况？若存在，求出此时AP的长；若不存在，请说明理由．

查看试题解析
23. 已知抛物线y=3ax²+2bx+c

(1)、若a=b=1，c=﹣1求该抛物线与x轴的交点坐标；

(2)、若a= $\frac{1}{3}$ ，c=2+b且抛物线在﹣2≤x≤2区间上的最小值是﹣3，求b的值；

(3)、若a+b+c=1，是否存在实数x，使得相应的y的值为1，请说明理由．

查看试题解析

2017年浙江省杭州市萧山区瓜沥片中考数学模拟试卷（3月份）

一、仔细选一选

二、 认真填一填

三、 全面答一答

二、认真填一填

三、全面答一答