2017年山东省泰安市东平县中考数学一模试卷
试卷更新日期:2017-04-26 类型:中考模拟
一、选择题
-
1. 计算(﹣π)0÷(﹣ )﹣2的结果是( )A、﹣ B、0 C、6 D、2. 下列计算正确的是( )A、2+a=2a B、2a﹣3a=﹣1 C、(﹣a)2•a3=a5 D、8ab÷4ab=2ab3.
下列图形:任取一个既是轴对称图形又是中心对称图形的概率是( )
 A、 B、 C、 D、14. 化简x÷•的结果为( )A、 B、 C、xy D、15. 某种细菌直径约为0.00000067mm,若将0.000 000 67mm用科学记数法表示为6.7×10nmm(n为负整数),则n的值为( )A、﹣5 B、﹣6 C、﹣7 D、﹣86. 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
A、 B、 C、 D、14. 化简x÷•的结果为( )A、 B、 C、xy D、15. 某种细菌直径约为0.00000067mm,若将0.000 000 67mm用科学记数法表示为6.7×10nmm(n为负整数),则n的值为( )A、﹣5 B、﹣6 C、﹣7 D、﹣86. 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( ) A、圆锥的底面半径为3 B、tanα= C、圆锥的表面积为12π D、该圆锥的主视图的面积为87. 如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
A、圆锥的底面半径为3 B、tanα= C、圆锥的表面积为12π D、该圆锥的主视图的面积为87. 如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( ) A、1:4 B、1:3 C、1:2 D、1:18. 如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
A、1:4 B、1:3 C、1:2 D、1:18. 如图,数轴上的A,B,C三点所表示的数是分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( ) A、点A的左边 B、点A与点B之间 C、点B与点C之间 D、点B与点C之间(靠近点C)或点C的右边9. 若5k+20<0,则关于x的一元二次方程x2+4x﹣k=0的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断10. 在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:
A、点A的左边 B、点A与点B之间 C、点B与点C之间 D、点B与点C之间(靠近点C)或点C的右边9. 若5k+20<0,则关于x的一元二次方程x2+4x﹣k=0的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断10. 在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
人数
1
3
3
4
3
2
这些运动员跳高成绩的中位数和众数分别是( )
A、1.70,1.65 B、1.70,1.70 C、1.65,1.70 D、3,311. 如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( ) A、 cm B、 cm C、 cm D、4cm12. 一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y= (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
A、 cm B、 cm C、 cm D、4cm12. 一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y= (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( ) A、b=2a+k B、a=b+k C、a>b>0 D、a>k>013. 甲计划用若干个工作日完成某项工作,从第二个工作日起,乙加入此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成此项工作的天数是( )A、8 B、7 C、6 D、514. 不等式组 的最小整数解为( )A、﹣1 B、0 C、1 D、215. 在﹣1,0,1,2,3这五个数中任取两数m,n,则二次函数y=﹣(x+m)2﹣n的顶点在x轴上的概率为( )A、 B、 C、 D、16.
A、b=2a+k B、a=b+k C、a>b>0 D、a>k>013. 甲计划用若干个工作日完成某项工作,从第二个工作日起,乙加入此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成此项工作的天数是( )A、8 B、7 C、6 D、514. 不等式组 的最小整数解为( )A、﹣1 B、0 C、1 D、215. 在﹣1,0,1,2,3这五个数中任取两数m,n,则二次函数y=﹣(x+m)2﹣n的顶点在x轴上的概率为( )A、 B、 C、 D、16.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1: ,则AB的长为( )
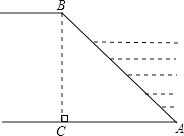 A、12米 B、4 米 C、5 米 D、6 米17. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A、12米 B、4 米 C、5 米 D、6 米17. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )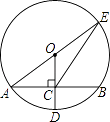 A、2 B、8 C、2 D、218. 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )
A、2 B、8 C、2 D、218. 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( ) A、40° B、60° C、70° D、80°19. 某商品的标价比成本价高m%,根据市场需要,该商品需降价n%出售,为了不亏本,n应满足( )A、n≤m B、n≤ C、n≤ D、n≤20.
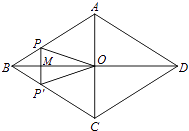
A、40° B、60° C、70° D、80°19. 某商品的标价比成本价高m%,根据市场需要,该商品需降价n%出售,为了不亏本,n应满足( )A、n≤m B、n≤ C、n≤ D、n≤20.如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
 A、
A、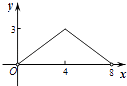 B、
B、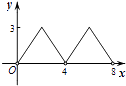 C、
C、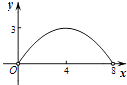 D、
D、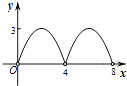
二、 填空题
-
21. 抛物线y=x2+mx+n可以由抛物线y=x2向下平移2个单位,再向右平移3个单位得到,则mn值为 .22. 如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为 .
 23. 如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN的长度为 .
23. 如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AN的长度为 . 24.
24.如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是 .

三、 解答题
-
25.
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
 (1)、求反比例函数的解析式;(2)、观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;(3)、若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.26. 山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?27. 已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)、求反比例函数的解析式;(2)、观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;(3)、若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.26. 山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?27. 已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P. (1)、当点P在线段AB上时,求证:△AQP∽△ABC;(2)、当△PQB为等腰三角形时,求AP的长.28. 如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)、当点P在线段AB上时,求证:△AQP∽△ABC;(2)、当△PQB为等腰三角形时,求AP的长.28. 如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F. (1)、证明:∠BAE=∠FEC;(2)、证明:△AGE≌△ECF;(3)、求△AEF的面积.29.
(1)、证明:∠BAE=∠FEC;(2)、证明:△AGE≌△ECF;(3)、求△AEF的面积.29.已知:如图一次函数y= x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
 (1)、求二次函数的解析式;(2)、求四边形BDEC的面积S;(3)、在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
(1)、求二次函数的解析式;(2)、求四边形BDEC的面积S;(3)、在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.