2017年辽宁省鞍山市铁西区中考数学五模试卷
试卷更新日期:2017-04-26 类型:中考模拟
一、选择题
-
1. 函数y= 的自变量x的取值范围是( )A、x≥﹣2 B、x≥﹣2且x≠0 C、x≠0 D、x>0且x≠﹣22. 一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、4,则第5组的频率是( )A、0.1 B、0.2 C、0.3 D、0.43. 已知二次函数y=﹣(x﹣a)2﹣b的图象如图所示,则反比例函数y= 与一次函数y=ax+b的图象可能是( )
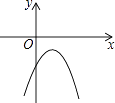 A、
A、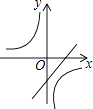 B、
B、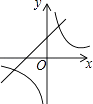 C、
C、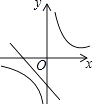 D、
D、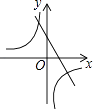 4. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
4. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )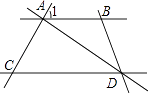 A、65° B、55° C、45° D、35°5. 已知正六边形的边长为2,则它的内切圆的半径为( )A、1 B、 C、2 D、26. 如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
A、65° B、55° C、45° D、35°5. 已知正六边形的边长为2,则它的内切圆的半径为( )A、1 B、 C、2 D、26. 如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) A、 = B、AD,AE将∠BAC三等分 C、△ABE≌△ACD D、S△ADH=S△CEG7. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
A、 = B、AD,AE将∠BAC三等分 C、△ABE≌△ACD D、S△ADH=S△CEG7. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )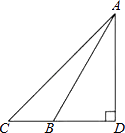 A、2 m B、2 m C、(2 ﹣2)m D、(2 ﹣2)m
A、2 m B、2 m C、(2 ﹣2)m D、(2 ﹣2)m二、 填空题
-
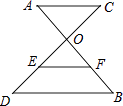
8. 当x=时,分式 的值为0.9. 分解因式:(2a+b)2﹣(a+2b)2= .10. 要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是运动员.(填“甲”或“乙”)11. 已知x1 , x2是关于x的方程x2+ax﹣2b=0的两实数根,且x1+x2=﹣2,x1•x2=1,则ba的值是 .12. 如图,AB、CD相交于点O,OC=2,OD=3,AC∥BD,EF是△ODB的中位线,且EF=2,则AC的长为 .
 13. 如图,菱形ABCD的面积为120cm2 , 正方形AECF的面积为50cm2 , 则菱形的边长为 cm.
13. 如图,菱形ABCD的面积为120cm2 , 正方形AECF的面积为50cm2 , 则菱形的边长为 cm.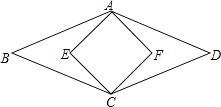 14. 如图,扇形OAB的圆心角为124°,C是弧 上一点,则∠ACB= .
14. 如图,扇形OAB的圆心角为124°,C是弧 上一点,则∠ACB= .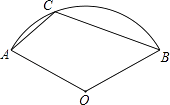 15. 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为 .
15. 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为 .
三、 解答题
-
16. 先化简,再求值: ÷(1﹣ ),其中x= .17. 如图,在▱ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.
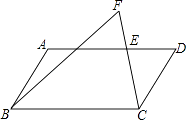 (1)、求证:∠D=∠F;(2)、用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).18. 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
(1)、求证:∠D=∠F;(2)、用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).18. 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.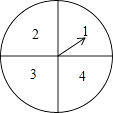 (1)、试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;(2)、某顾客参加一次抽奖,能获得返还现金的概率是多少?19. 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)、试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;(2)、某顾客参加一次抽奖,能获得返还现金的概率是多少?19. 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E. (1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.
(1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.四、 解答题
-
20. 图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ,tan ,以O为原点,OA所在直线为x轴建立直角坐标系.
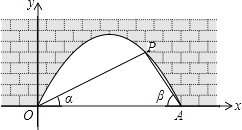 (1)、求点P的坐标;(2)、水面上升1m,水面宽多少( 取1.41,结果精确到0.1m)?21. 如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)、求点P的坐标;(2)、水面上升1m,水面宽多少( 取1.41,结果精确到0.1m)?21. 如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.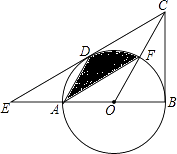 (1)、求证:CB是⊙O的切线;(2)、若∠ECB=60°,AB=6,求图中阴影部分的面积.22. 如图,反比例函数y= 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
(1)、求证:CB是⊙O的切线;(2)、若∠ECB=60°,AB=6,求图中阴影部分的面积.22. 如图,反比例函数y= 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).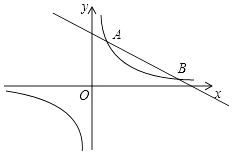 (1)、求反比例函数与一次函数的表达式;(2)、点E为y轴上一个动点,若S△AEB=10,求点E的坐标.23. 某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
(1)、求反比例函数与一次函数的表达式;(2)、点E为y轴上一个动点,若S△AEB=10,求点E的坐标.23. 某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:产品
每件售价(万元)
每件成本(万元)
每年其他费用(万元)
每年最大产销量(件)
甲
6
a
20
200
乙
20
10
40+0.05x2
80
其中a为常数,且3≤a≤5
(1)、若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;(2)、分别求出产销两种产品的最大年利润;(3)、为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.