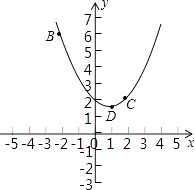2017年湖南省娄底市新化县中考数学一模试卷

试卷更新日期：2017-04-26 类型：中考模拟

进入出卷网下载

一、选择题

1. 2017的倒数是（）

A、 $\frac{1}{2017}$ B、﹣ $\frac{1}{2017}$ C、2017 D、﹣2017

查看试题解析
2. 关于 $\sqrt{12}$ 的叙述，错误的是（）

A、 $\sqrt{12}$ 是有理数 B、面积为12的正方形边长是 $\sqrt{12}$ C、 $\sqrt{12}$ =2 $\sqrt{3}$ D、在数轴上可以找到表示 $\sqrt{12}$ 的点

查看试题解析
3. 把多项式x²+ax+b分解因式，得（x+1）（x﹣3）则a，b的值分别是（）

A、a=2，b=3 B、a=﹣2，b=﹣3 C、a=﹣2，b=3 D、a=2，b=﹣3

查看试题解析
4. 科学家在实验中检测出某微生物约为0.0000025米，将0.0000025用科学记数法表示为（）

A、2.5×10^﹣⁶ B、2.5×10⁶ C、2.5×10^﹣⁵ D、25×10^﹣⁵

查看试题解析
5. 不等式组 ${\begin{matrix} x - 3 < 1 \\ 3 x + 2 \leq 4 x \end{matrix}$ 的解集为（）

A、x≤2 B、x＜4 C、2≤x＜4 D、x≥2

查看试题解析
6. 下列算式
① $\sqrt{9}$ =±3；② ${(- \frac{1}{3})}^{- 2}$ =9；③2⁶÷2³=4；④ ${(\sqrt{- 2016})}^{2}$ =2016；⑤a+a=a² ．
运算结果正确的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. 反比例函数y=﹣ $\frac{3}{x}$ 的图象上有P₁（x₁ ， ﹣2），P₂（x₂ ， ﹣3）两点，则x₁与x₂的大小关系是（）

A、x₁＜x₂ B、x₁=x₂ C、x₁＞x₂ D、不确定

查看试题解析
8. 已知抛物线y=﹣x²﹣2x+3与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、2

查看试题解析
9. 如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）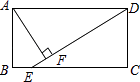

A、△AFD≌△DCE B、AF= $\frac{1}{2}$ AD C、AB=AF D、BE=AD﹣DF

查看试题解析
10. 在△ABC中，AB=10，AC=2 $\sqrt{10}$ ，BC边上的高AD=6，则另一边BC等于（）

A、10 B、8 C、6或10 D、8或10

查看试题解析
11. 宜宾市某化工厂，现有A种原料52千克，B种原料64千克，现用这些原料生产甲、乙两种产品共20件．已知生产1件甲种产品需要A种原料3千克，B种原料2千克；生产1件乙种产品需要A种原料2千克，B种原料4千克，则生产方案的种数为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

12. 若式子 $\sqrt{x - 1}$ 有意义，则实数x的取值范围是．

查看试题解析
13. 一组数据2，4，a，7，7的平均数 $\bar{x}$ =5，则方差S²= ．

查看试题解析
14. 设x₁ ， x₂是方程5x²﹣3x﹣1=0的两个实数根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为．

查看试题解析
15. 如图，直线a∥b，∠1=85°，∠2=35°，则∠3为．

查看试题解析
16. 如图，在Rt△ABC中，∠C=90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E，若BC=3，则DE的长为．

查看试题解析
17. 在平面直角坐标系中，直线l：y=x﹣1与x轴交于点A₁ ，如图所示依次作正方形A₁B₁C₁O、正方形A₂B₂C₂C₁、…、正方形A_nB_nC_nC_n_﹣₁ ，使得点A₁、A₂、A₃、…在直线l上，点C₁、C₂、C₃、…在y轴正半轴上，则点B_n的坐标是．

查看试题解析

三、解答题

18. 计算；（﹣1）²⁰¹⁷+2sin60°﹣|﹣ $\sqrt{3}$ |﹣（π﹣2017）⁰ ．

查看试题解析
19. 已知4x=3y，求代数式（x﹣2y）²﹣（x﹣y）（x+y）﹣2y²的值．

查看试题解析
20.
某地的一座人行天桥如图所示，天桥高为6米，坡面BC的坡度为1：1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1： $\sqrt{3}$ ．

(1)、求新坡面的坡角a；

(2)、原天桥底部正前方8米处（PB的长）的文化墙PM是否需要拆除？请说明理由．

查看试题解析
21. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的5个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：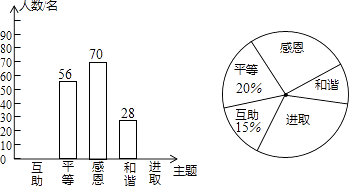

(1)、这次调查的学生共有多少名？

(2)、请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．

(3)、如果要在这5个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．

查看试题解析
22. 已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．

(1)、求证：△ABF≌△CDE；

(2)、如图，若∠1=65°，求∠B的大小．

查看试题解析
23. 早晨，小明步行到离家900米的学校去上学，到学校时发现眼镜忘在家中，于是他立即按原路步行回家，拿到眼镜后立即按原路骑自行车返回学校．已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟，小明骑自行车速度是步行速度的3倍．

(1)、求小明步行速度（单位：米/分）是多少；

(2)、下午放学后，小明骑自行车回到家，然后步行去图书馆，如果小明骑自行车和步行的速度不变，小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍，那么小明家与图书馆之间的路程最多是多少米？

查看试题解析
24. 如图，在Rt△ABC中，∠C=90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E．

(1)、求证：AC是⊙O的切线；

(2)、若OB=10，CD=8，求BE的长．

查看试题解析
25. 在平面直角坐标系xOy中，抛物线y=ax²+bx+2过B（﹣2，6），C（2，2）两点．

(1)、试求抛物线的解析式；

(2)、记抛物线顶点为D，求△BCD的面积；

(3)、若直线y=﹣ $\frac{1}{2}$ x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．

查看试题解析

2017年湖南省娄底市新化县中考数学一模试卷

一、选择题

二、 填空题

三、 解答题

二、填空题

三、解答题