2017年湖北省孝感市中考数学模拟试卷

试卷更新日期：2017-04-26 类型：中考模拟

进入出卷网下载

一、精心选一选

1. 一元二次方程x²+x﹣1=0 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
2. 下列图形中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 甲、乙、丙3人聚会，每人带了一件从外盒包装上看完全相同的礼物（里面的东西只有颜色不同），将3件礼物放在一起，每人从中随机抽取一件．则下列事件是必然事件的是（）

A、乙抽到一件礼物 B、乙恰好抽到自己带来的礼物 C、乙没有抽到自己带来的礼物 D、只有乙抽到自己带来的礼物

查看试题解析
4. 如果反比例函数y= $\frac{m + 1}{x}$ 在各自象限内，y随x的增大而减小，那么m的取值范围是（）

A、m＜0 B、m＞0 C、m＜﹣1 D、m＞﹣1

查看试题解析
5. 已知圆锥的底面半径为4，母线长为12，则圆锥的侧面展开图的圆心角为（）

A、60° B、90° C、120° D、216°

查看试题解析
6. 抛物线y=2x²﹣3的顶点在（）

A、第一象限 B、第二象限 C、x轴上 D、y轴上

查看试题解析
7. 如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（）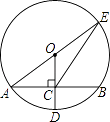

A、2 $\sqrt{15}$ B、8 C、2 $\sqrt{10}$ D、2 $\sqrt{13}$

查看试题解析
8. 从2，3，4，5中任意选两个数，记作a和b，那么点（a，b）在函数y= $\frac{12}{x}$ 图象上的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
9. 如图，已知△ABC中，AC=BC，∠ACB=90°，直角∠DFE的顶点F是AB中点，两边FD，FE分别交AC，BC于点D，E两点，当∠DFE在△ABC内绕顶点F旋转时（点D不与A，C重合），给出以下个结论：①CD=BE ②四边形CDFE不可能是正方形 ③△DFE是等腰直角三角形 ④S_四边形_CDFE= $\frac{1}{2}$ S_△_ABC ，上述结论中始终正确的有（）

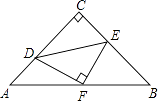A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析
10. 如图，二次函数y=ax²+bx+c的图象与y轴正半轴相交，其顶点坐标为（ $\frac{1}{2}$ ，1），下列结论：①ac＜0；②a+b=0；③4ac﹣b²=4a；④a+b+c＜0．其中正确结论的个数是（）

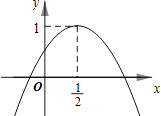A、1 B、2 C、3 D、4

查看试题解析

二、细心填一填

11. 若一三角形的三边长分别为5、12、13，则此三角形的内切圆半径为．

查看试题解析
12. 三张完全相同的卡片上分别写有函数y=﹣2x﹣3，y= $\frac{3}{x}$ ，y=x²+1，从中随机抽取一张，则所得函数的图象在第一象限内y随x的增大而增大的概率是．

查看试题解析
13.
如图，某小区规划在一个长为16m、宽为9m的矩形场地ABCD上修建三条同样宽的小路，使其中两条与AB平行，另一条与AD平行，其余部分种草．若草坪部分的总面积为112m² ，求小路的宽度．若设小路的宽度为xm，则x满足的方程为．

查看试题解析
14. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A₁B₁C，连结AA₁ ，若∠AA₁B₁=15°，则∠B的度数是．

查看试题解析
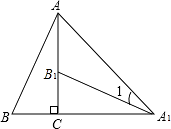15. 设函数y=x+5与y= $\frac{3}{x}$ 的图象的两个交点的横坐标为a、b，则 $\frac{1}{a} + \frac{1}{b}$ 的值是．

查看试题解析
16. 抛物线y=ax²+bx+c的顶点为D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b²﹣4ac＜0；②a+b+c＜0；③c﹣a=2；④方程ax²+bx+c﹣2=0有两个相等的实数根．其中正确的结论有（填序号）．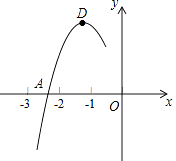

查看试题解析

三、用心做一做

17. 解下列方程：

(1)、2x²﹣x=1

(2)、x²+4x+2=0．

查看试题解析
18. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣6，0），B（﹣1，1），C（﹣3，3），将△ABC绕点B顺时针方向旋转90°后得到△A₁BC₁ ．

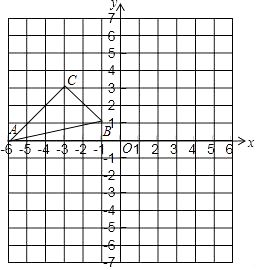(1)、画出△A₁BC₁ ，写出点A₁、C₁的坐标；

(2)、计算线段BA扫过的面积．

查看试题解析
19. 不透明的口袋里装有红、黄、蓝三种颜色的小球（除颜色不同外，其它都一样），其中红球2个，蓝球1个，现在从中任意摸出一个红球的概率为 $\frac{1}{2}$ ．

(1)、求袋中黄球的个数；

(2)、第一次摸出一个球（不放回），第二次再摸出一个球，请用树状图或列表法求两次摸出的都是红球的概率．

查看试题解析
20. 如图，四边形ABCD中，∠ABC=∠ADC=90°，BD⊥AC，垂足为P．

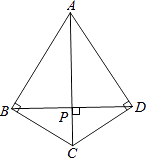(1)、请作出Rt△ABC的外接圆⊙O；（保留作图痕迹，不写作法）

(2)、点D在⊙O上吗？说明理由；

(3)、试说明：AC平分∠BAD．

查看试题解析
21. 如图，一次函数与反比例函数y= $\frac{m}{x}$ 的图象交于A（1，4），B（4，n）两点．

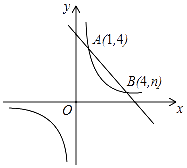(1)、求反比例函数的解析式；

(2)、点P是x轴上的一动点，试确定点P使PA+PB最小，并求出点P的坐标．

查看试题解析
22. 已知关于x的一元二次方程：x²﹣2（m+1）x+m²+5=0有两个不相等的实数根．

(1)、求m的取值范围；

(2)、若原方程的两个实数根为x₁、x₂ ，且满足x₁²+x₂²=|x₁|+|x₂|+2x₁x₂ ，求m的值．

查看试题解析
23. 如图，△ABC内接于⊙O，AD平分∠BAC交⊙O于点D，过点D作DE∥BC交AC的延长线于点E．

(1)、试判断DE与⊙O的位置关系，并证明你的结论；

(2)、若∠E=60°，⊙O的半径为5，求AB的长．

查看试题解析
24.
如图，抛物线y=﹣ $\frac{1}{2}$ x²+bx+c与一次函数y=﹣x+4分别交y轴、x轴于A、B两点．

(1)、求这个抛物线的解析式；

(2)、设P（x，y）是抛物线在第一象限内的一个动点，过点P作直线PH⊥x轴于点H，交直线AB于点M．
①求当x取何值时，PM有最大值？最大值是多少？
②当PM取最大值时，以A、P、M、N为顶点构造平行四边形，求第四个顶点N的坐标．

查看试题解析

2017年湖北省孝感市中考数学模拟试卷

一、精心选一选

二、 细心填一填

三、 用心做一做

二、细心填一填

三、用心做一做