2017年湖北省黄石市大冶市中考数学模拟试卷(3月份)
试卷更新日期:2017-04-26 类型:中考模拟
一、仔细选一选
-
1. 实数﹣17的相反数是( )A、17 B、 C、﹣17 D、﹣2. 在下列四个图案中,既是轴对称图形,又是中心对称图形是( )A、
 B、
B、 C、
C、 D、
D、 3. 地球上的陆地面积约为149000000km2 . 将149000000用科学记数法表示为( )A、1.49×106 B、1.49×107 C、1.49×108 D、1.49×1094. 下列命题错误的是( )A、对角线互相垂直平分的四边形是菱形 B、平行四边形的对角线互相平分 C、矩形的对角线相等 D、对角线相等的四边形是矩形5. 下列运算正确的是( )A、3﹣1=﹣3 B、 =±3 C、(ab2)3=a3b6 D、a6÷a2=a36. 在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )A、平均数为160 B、中位数为158 C、众数为158 D、方差为20.37. 如图的几何体的俯视图是( )
3. 地球上的陆地面积约为149000000km2 . 将149000000用科学记数法表示为( )A、1.49×106 B、1.49×107 C、1.49×108 D、1.49×1094. 下列命题错误的是( )A、对角线互相垂直平分的四边形是菱形 B、平行四边形的对角线互相平分 C、矩形的对角线相等 D、对角线相等的四边形是矩形5. 下列运算正确的是( )A、3﹣1=﹣3 B、 =±3 C、(ab2)3=a3b6 D、a6÷a2=a36. 在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )A、平均数为160 B、中位数为158 C、众数为158 D、方差为20.37. 如图的几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=( )
8. 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=( )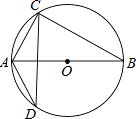 A、 B、 C、 D、9.
A、 B、 C、 D、9.如图是二次函数y=ax2+bx+c的图象,下列结论:
①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;
③一元二次方程ax2+bx+c=1的两根之和为﹣1;
④使y≤3成立的x的取值范围是x≥0.
其中正确的个数有( )
 A、1个 B、2个 C、3个 D、4个10. 如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D,E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时.设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )
A、1个 B、2个 C、3个 D、4个10. 如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D,E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时.设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )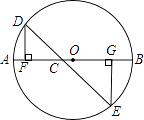 A、
A、 B、
B、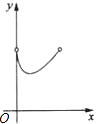 C、
C、 D、
D、
二、 认真填一填:
-
11. 分解因式:a3﹣4a2+4a= .12. 已知关于x的一元二次方程x2+ax+b=0有一个非零根﹣b,则a﹣b的值为 .13. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为 .
 14. 小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有人.
14. 小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有人. 15. 将函数y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|2x+b|(b为常数)的图象.若该图象在直线y=2下方的点的横坐标x满足0<x<3,则b的取值范围为 .16. 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,那么S3= , 则Sn= . (用含n的式子表示)
15. 将函数y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|2x+b|(b为常数)的图象.若该图象在直线y=2下方的点的横坐标x满足0<x<3,则b的取值范围为 .16. 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,那么S3= , 则Sn= . (用含n的式子表示)
三、 全面答一答
-
17. 计算: +( )﹣2+| ﹣1|﹣2sin60°.18. 先化简,再求值: ÷( + ),其中x=2.19. 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC= OB.
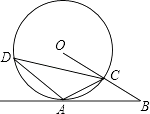 (1)、求证:AB是⊙O的切线;(2)、若∠ACD=45°,OC=2,求弦CD的长.20. 解不等式组: ,并在数轴上表示出不等式组的解集.21. 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.
(1)、求证:AB是⊙O的切线;(2)、若∠ACD=45°,OC=2,求弦CD的长.20. 解不等式组: ,并在数轴上表示出不等式组的解集.21. 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
 (1)、嘉嘉随机掷一次骰子,求落回到圈A的概率P1;(2)、淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?22. 如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).
(1)、嘉嘉随机掷一次骰子,求落回到圈A的概率P1;(2)、淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?22. 如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
 23. 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
23. 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).时间x(天)
1
30
60
90
每天销售量p(件)
198
140
80
20
 (1)、求出w与x的函数关系式;(2)、问销售该商品第几天时,当天的销售利润最大?并求出最大利润;(3)、该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.24. 如图1,在菱形ABCD中,AC=2,BD=2 ,AC,BD相交于点O.
(1)、求出w与x的函数关系式;(2)、问销售该商品第几天时,当天的销售利润最大?并求出最大利润;(3)、该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.24. 如图1,在菱形ABCD中,AC=2,BD=2 ,AC,BD相交于点O. (1)、求边AB的长;(2)、如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
(1)、求边AB的长;(2)、如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
25. 已知双曲线y= (x>0),直线l1:y﹣ =k(x﹣ )(k<0)过定点F且与双曲线交于A,B两点,设A(x1 , y1),B(x2 , y2)(x1<x2),直线l2:y=﹣x+ . (1)、若k=﹣1,求△OAB的面积S;(2)、若AB= ,求k的值;(3)、设N(0,2 ),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形?若存在,请求出Q点的坐标.
(1)、若k=﹣1,求△OAB的面积S;(2)、若AB= ,求k的值;(3)、设N(0,2 ),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形?若存在,请求出Q点的坐标.