2017年安徽省合肥市瑶海区中考数学一模试卷
试卷更新日期:2017-04-26 类型:中考模拟
一、选择题
-
1. 在﹣2,﹣5,5,0这四个数中,最小的数是( )A、﹣2 B、﹣5 C、5 D、02. 据统计2014年我国高新技术产品出口总额40570亿元,将数据40570亿用科学记数法表示为( )A、4.0570×109 B、0.40570×1010 C、40.570×1011 D、4.0570×10123. 如图,直线l1∥l2 , CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
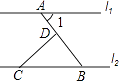 A、50° B、45° C、40° D、30°4. 不等式组﹣2≤x+1<1的解集,在数轴上表示正确的是( )A、
A、50° B、45° C、40° D、30°4. 不等式组﹣2≤x+1<1的解集,在数轴上表示正确的是( )A、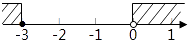 B、
B、 C、
C、 D、
D、 5. 过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥所得到的几何体如图所示,它的俯视图为( )
5. 过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥所得到的几何体如图所示,它的俯视图为( )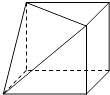 A、
A、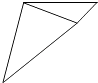 B、
B、 C、
C、 D、
D、 6. 如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
6. 如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( ) A、 B、 C、 D、7. 某工厂二月份的产值比一月份的产值增长了x%,三月份的产值又比二月份的产值增长了x%,则三月份的产值比一月份的产值增长了( )A、2x% B、1+2x% C、(1+x%)x% D、(2+x%)x%8. 如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于( )
A、 B、 C、 D、7. 某工厂二月份的产值比一月份的产值增长了x%,三月份的产值又比二月份的产值增长了x%,则三月份的产值比一月份的产值增长了( )A、2x% B、1+2x% C、(1+x%)x% D、(2+x%)x%8. 如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于( )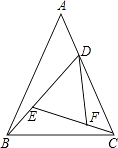 A、 B、 C、 D、
A、 B、 C、 D、二、 填空题
-
9. 分解因式:m3n﹣4mn= .10. 若函数y= 与y=x﹣2图象的一个交点坐标(a,b),则 的值为 .11. 一组数:2,1,3,x,7,y,23,…,满足“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b”,例如这组数中的第三个数“3”是由“2×2﹣1”得到的,那么这组数中y表示的数为 .12. 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;②线段BF的取值范围为3≤BF≤4;
③EC平分∠DCH;④当点H与点A重合时,EF=2
以上结论中,你认为正确的有 . (填序号)

三、 解答题
-
13. 计算:﹣22﹣ +2cos45°+|1﹣ |14. 如图,一次函数的图象经过(2,0)和(0,﹣4),根据图象求 的值.
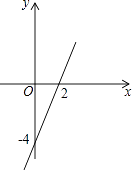 15.
15.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
 (1)、请按下列要求画图:
(1)、请按下列要求画图:①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1 , 画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2 .
(2)、在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.16. 有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.(1)、请用树状图或列表的方法求这三条线段能组成三角形的概率;(2)、求这三条线段能组成直角三角形的概率.17. 已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求: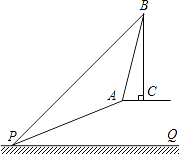 (1)、坡顶A到地面PQ的距离;(2)、古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)18. 如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2 .
(1)、坡顶A到地面PQ的距离;(2)、古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)18. 如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2 .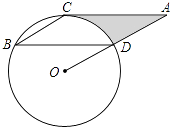 (1)、求证:AC是⊙O的切线;(2)、求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)19. 如图甲,AB⊥BD,CD⊥BD,AP⊥PC,垂足分别为B、P、D,且三个垂足在同一直线上,我们把这样的图形叫“三垂图”.
(1)、求证:AC是⊙O的切线;(2)、求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)19. 如图甲,AB⊥BD,CD⊥BD,AP⊥PC,垂足分别为B、P、D,且三个垂足在同一直线上,我们把这样的图形叫“三垂图”.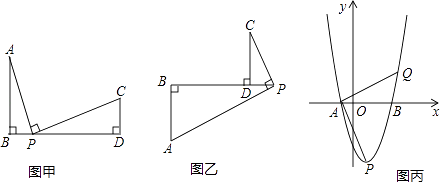 (1)、证明:AB•CD=PB•PD.(2)、如图乙,也是一个“三垂图”,上述结论成立吗?请说明理由.(3)、已知抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点(0,﹣3),顶点为P,如图丙所示,若Q是抛物线上异于A、B、P的点,使得∠QAP=90°,求Q点坐标.20. 某网店打出促销广告:最潮新款服装50件,每件售价300元,若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低2元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.(1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、顾客一次性购买多少件时,该网店从中获利最多?21. 在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
(1)、证明:AB•CD=PB•PD.(2)、如图乙,也是一个“三垂图”,上述结论成立吗?请说明理由.(3)、已知抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点(0,﹣3),顶点为P,如图丙所示,若Q是抛物线上异于A、B、P的点,使得∠QAP=90°,求Q点坐标.20. 某网店打出促销广告:最潮新款服装50件,每件售价300元,若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低2元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.(1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、顾客一次性购买多少件时,该网店从中获利最多?21. 在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
(Ⅰ)如图①,当α=90°时,求AE′,BF′的长;
(Ⅱ)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
(Ⅲ)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).