河北省保定市安国市2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-03-14 类型:期中考试
一、选择题
-
1. 的立方根是( )A、4 B、2 C、 D、82. 点P(-5,3)关于y轴的对称点的坐标是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列长度的三条线段不能组成直角三角形的是( )A、1, , B、 ,
3. 下列长度的三条线段不能组成直角三角形的是( )A、1, , B、 ,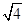 ,
C、5,4,3
D、 ,2,
,
C、5,4,3
D、 ,2, 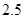 4. 如图,点A(-1,2),则点B的坐标为( )
4. 如图,点A(-1,2),则点B的坐标为( ) A、
A、 B、
B、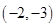 C、
C、 D、
D、 5. 下列二次根式中是最简二次根式的是( )A、 B、
5. 下列二次根式中是最简二次根式的是( )A、 B、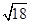 C、
C、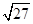 D、
D、 6. 下列运算正确的是( )A、
6. 下列运算正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 设 的小数部分为b,则b(b+3)的值是( )A、1 B、
7. 设 的小数部分为b,则b(b+3)的值是( )A、1 B、 C、3
D、无法确定
8. 在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是( )。A、5 B、4 C、3 D、29. 一次函数y=kx-1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )A、
C、3
D、无法确定
8. 在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是( )。A、5 B、4 C、3 D、29. 一次函数y=kx-1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )A、 B、
B、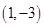 C、
C、 D、
D、 10. 如图,直线l是一次函数y=kx+b的图象,若点A(3,m)在直线l上,则m的值是( )
10. 如图,直线l是一次函数y=kx+b的图象,若点A(3,m)在直线l上,则m的值是( ) A、
A、 B、
C、
B、
C、 D、7
11. 如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0, ).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是( )
D、7
11. 如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0, ).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是( ) A、
A、 B、
B、 C、
C、 D、
D、 12. 如图,利用三个面积分别为5,x,y的正方形拼成一个直角三角形,则y关于x之间的函数图象不经过( )
12. 如图,利用三个面积分别为5,x,y的正方形拼成一个直角三角形,则y关于x之间的函数图象不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限13. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个锐角顶点与另一个的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一条直线上,若AB= ,则CD的长为( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限13. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个锐角顶点与另一个的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一条直线上,若AB= ,则CD的长为( )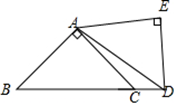 A、 B、 C、
A、 B、 C、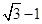 D、
14. 如图:三个正比例函数的图象分别对应的解析式是①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是( )
D、
14. 如图:三个正比例函数的图象分别对应的解析式是①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是( )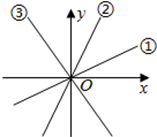 A、
A、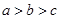 B、
B、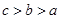 C、
C、 D、
D、 15. 如图中表示一次函数y=mx+n与正比例函数y=mnx(m、n是常数,mn≠0)图象的是( )A、
15. 如图中表示一次函数y=mx+n与正比例函数y=mnx(m、n是常数,mn≠0)图象的是( )A、 B、
B、 C、
C、 D、
D、 16. 如图,在平面直角坐标系中,点M是直线y=-x上的点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为( )
16. 如图,在平面直角坐标系中,点M是直线y=-x上的点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为( ) A、 B、
A、 B、 C、
C、 D、
D、
二、填空题
-
17. 若点A(a+1,b-2)在第二象限,则点B(-a,1-b)在第象限.18. 如图,圆柱形玻璃杯高为13cm,底面周长为40cm,在杯内壁离底1cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁到内壁B处的最短距离为 .
 19. 汽车行驶前,油箱中有油55L,已知每百千米汽车耗油10L,油箱中的余油量Q(L)与它行驶的距离s(百千米)之间的函数关系式为 , 为了保证行车安全,油箱中至少存油5L.则汽车最多可行驶km.
19. 汽车行驶前,油箱中有油55L,已知每百千米汽车耗油10L,油箱中的余油量Q(L)与它行驶的距离s(百千米)之间的函数关系式为 , 为了保证行车安全,油箱中至少存油5L.则汽车最多可行驶km.三、计算题
-
20. 计算下列各题(1)、 ×( -1)(2)、2×21. 某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.(1)、分别写出两种方式所花费用y(元)与游泳次数x(次)之间的函数关系式;(2)、若洋洋今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?(3)、游泳多少次时,洋洋选择两种方式付费相同?(4)、优优说今年夏季我最多游泳20次,他选择哪种方式更合算?并说明理由.
四、解答题
-
22. 如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
 23. 已知y-4与x成正比,当x=1时,y=2
23. 已知y-4与x成正比,当x=1时,y=2 (1)、求y与x之间的函数关系式,在下列坐标系中画出函数图象;(2)、当x= 时,求函数y的值;(3)、结合图象和函数的增减性,求当y<-2时自变量x的取值范围.24. 嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1 , R2 , R3 , 其行经位置如图与表所示:
(1)、求y与x之间的函数关系式,在下列坐标系中画出函数图象;(2)、当x= 时,求函数y的值;(3)、结合图象和函数的增减性,求当y<-2时自变量x的取值范围.24. 嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1 , R2 , R3 , 其行经位置如图与表所示:路径
编号
图例
行径位置
第一条路径
R1

A→C→D→B
第二条路径
R2

A→E→D→F→B
第三条路径
R3

A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
 25. 观察下列各式及验证过程
25. 观察下列各式及验证过程= ,验证: = = = ;
= ,验证: = = = ;
= ,验证: = = = ;
(1)、按照上述三个等式及其验证过程的基本思路,猜想 =;(2)、按照上述三个等式及其验证过程的基本思路,猜想 的变形结果并进行验证;(3)、针对上述各式反映的规律,写出用n(n≥2的自然数)表示的等式,并进行验证.26. 在平面几何中,我们学过两条直线平行的定义,下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1 , 一次函数y=k2x+b2(k2≠0)的图象为直线l2 , 若k1=k2 , 且b1≠b2 , 我们就称直线l1与直线l2互相平行.解答下面的问题: (1)、求过点P(1,2),且与已知直线y=-2x-1平行的直线l的函数解析式,并画出图象;(2)、设直线l分别与y轴,x轴交于点A、B,如果直线m:y=kx+t(t>0)与直线l平行,且交x轴于点C,求出△ABC的面积S关于t函数关系式.
(1)、求过点P(1,2),且与已知直线y=-2x-1平行的直线l的函数解析式,并画出图象;(2)、设直线l分别与y轴,x轴交于点A、B,如果直线m:y=kx+t(t>0)与直线l平行,且交x轴于点C,求出△ABC的面积S关于t函数关系式.