2018-2019学年初中数学北师大版九年级下册3.8圆内接正多边形 同步练习
试卷更新日期：2019-03-13 类型：同步测试
一、单选题
-
1. 如图，正八边形ABCDEFGH中，∠EAG大小为（ ）
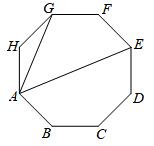
A、30° B、40° C、45° D、50°2. 以半径为1的圆内接正三角形，正方形，正六边形的边心距为三边作三角形，则该三角形的面积是（ ）A、 B、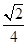
C、
D、
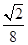3. 半径为r的圆的内接正三角形的边长是（ ）A、2r B、
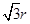C、
D、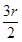
4. 如图，ABCDEF为⊙O的内接正六边形，AB=a，则图中阴影部分的面积是（ ）
A、 B、（ ）a2 C、 2 D、（ ）a25. 已知圆内接正三角形的面积为 ，则该圆的内接正六边形的边心距是（ ）A、 B、 C、 D、6. 如图，将正五边形绕其中心O顺时针旋转ɑ角度，与原正五边形构成新的图形，若要使该图形是中心对称图形，则ɑ的最小角度为（ ）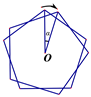
A、30° B、36° C、72° D、907. 如图，雯雯开了一家品牌手机体验店，想在体验区(图1阴影部分)摆放图2所示的正六边形桌子若干张．体验店平面图是长9米、宽7米的矩形，通道宽2米，桌子的边长为1米；摆放时要求桌子至少离墙1米，且有边与墙平行，桌子之间的最小距离至少1米，则体验区可以摆放桌子（ ）
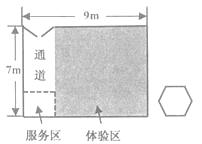A、4张 B、5张 C、6张 D、7张8. 正六边形的边心距与边长之比为（ ）
A、1 ： 2 B、：2 C、：1 D、：29. 以下说法正确的是（ ）A、每个内角都是120°的六边形一定是正六边形 B、正n边形的对称轴不一定有n条． C、正n边形的每一个外角度数等于它的中心角度数． D、正多边形一定既是轴对称图形，又是中心对称图形．二、填空题
-
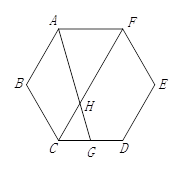
10. 如图，点G是正六边形ABCDEF的CD边的中点，AG与CF交于H点．则∠AHF+∠HGC=度，若AB=a，则FH=（用含a的代数式表示）．
11. 如图，边长相等的正五边形和正六边形拼接在一起，则∠ABC的度数为 ．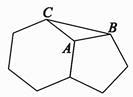
12. 如图，连接正十边形的对角线AC与BD交于点E，则∠AED＝°.
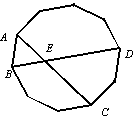13. 如图， 是半径为2的圆内接正三角形，则图中阴影部分的面积是 结果用含 的式子表示 ．
14. 刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.设⊙ 的半径为1，若用⊙ 的外切正六边形的面积 来近似估计⊙ 的面积，则 .（结果保留根号）15. 小明发现相机快门打开过程中，光圈大小变化如图1所示，于是他绘制了如图2所示的图形．图2中留个形状大小都相同的四边形围成一个圆的内接六边形和一个小正六边形，若PQ所在的直线经过点M，PB=5cm，小正六边形的面积为 cm2 ， 则该圆的半径为cm．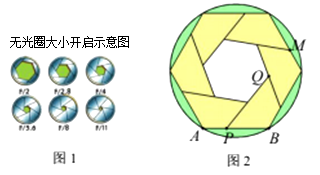
三、解答题
-
16. 如图，正方形ABCD的外接圆为⊙O，点P在劣弧 CD上（不与C点重合）．
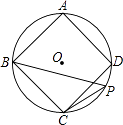(1)、求∠BPC的度数；
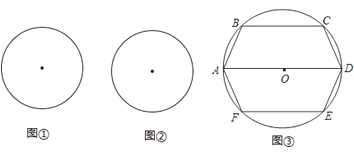
(2)、若⊙O的半径为8，求正方形ABCD的边长．17.如图，圆O的半径为r．
（1）在图①中，画出圆O的内接正△ABC，简要写出画法；求出这个正三角形的周长．
（2）在图②中，画出圆O的内接矩形ABCD，简要写出画法；若设AB=x，求出矩形的周长.
（3）如图③，六边形ABCDEF内接于半径为r（常数）的⊙O，其中AD为直径，且AB=CD=DE=FA．设AB=x，求六边形ABCDEF的周长L关于x的函数关系式，并探究L是否有最大值，若有，请指出x为何值时，L取得最大值；若没有，请说明理由．
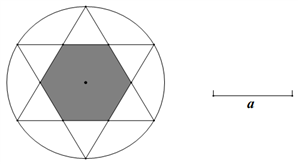
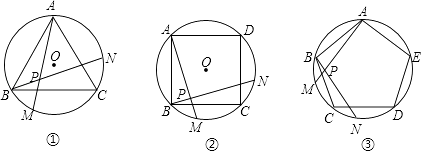
18. 如图，有一个圆O和两个正六边形T1 ， T2 ． T1的6个顶点都在圆周上，T2的6条边都和圆O相切（我们称T1 ， T2分别为圆O的内接正六边形和外切正六边形）．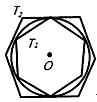
(1)、设T1 ， T2的边长分别为a，b，圆O的半径为r，求r：a及r：b的值；(2)、求正六边形T1 ， T2的面积比S1：S2的值．19. 如图，10－1、10－2、10－3、…、10－n分别是⊙O的内接正三角形ABC，正四边形ABCD，正五边形ABCDE，、…、正n边形ABCD…，点M、N分别从点B，C开始以相同的速度在⊙O上逆时针运动
(1)、求图10－1中∠APN的度数；
(2)、图10－2中，∠APN的度数是 ， 图10－3中∠BPN的度数是。
(3)、试探索∠APN的度数与正多边形边数n的关系（直接写答案）
20. 如图，⊙O半径为4cm，其内接正六边形ABCDEF，点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，连接PB，QE，PE，BQ．设运动时间为t（s）．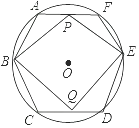
(1)、求证：四边形PEQB为平行四边形；(2)、填空：①当t=s时，四边形PBQE为菱形；
②当t=s时，四边形PBQE为矩形．
