2018-2019学年初中数学北师大版九年级下册3.7 切线长定理 同步练习
试卷更新日期:2019-03-13 类型:同步测试
一、单选题
-
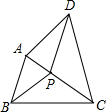
1. 如图,四边形ABCD中,∠A、∠B、∠C、∠D的角平分线恰相交于一点P,记△APD、△APB、△BPC、△DPC的面积分别为S1、S2、S3、S4 , 则有( )
 A、
A、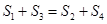 B、
B、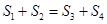 C、
C、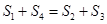 D、
D、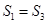 2. 如图,已知 是⊙ 的直径, , 和 是圆 的两条切线, , 为切点,过圆上一点 作⊙ 的切线 ,分别交 , 于点 , ,连接 , .若 ,则 等于( )
2. 如图,已知 是⊙ 的直径, , 和 是圆 的两条切线, , 为切点,过圆上一点 作⊙ 的切线 ,分别交 , 于点 , ,连接 , .若 ,则 等于( )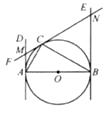 A、0.5 B、1 C、 D、3. 如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若BO=6cm,OC=8cm 则BE+CG的长等于( )
A、0.5 B、1 C、 D、3. 如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若BO=6cm,OC=8cm 则BE+CG的长等于( )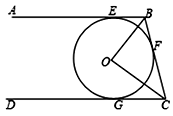 A、13 B、12 C、11 D、104. 如图,⊙ 与正方形 的两边 相切,且 与⊙ 相切于点 .若 , ,则⊙ 的半径为( )
A、13 B、12 C、11 D、104. 如图,⊙ 与正方形 的两边 相切,且 与⊙ 相切于点 .若 , ,则⊙ 的半径为( )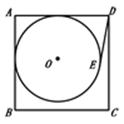 A、 B、 C、 D、5. 如图, 是四边形 的内切圆,下列结论一定正确的有( )个:
A、 B、 C、 D、5. 如图, 是四边形 的内切圆,下列结论一定正确的有( )个:① ;② ;③ ;④ .
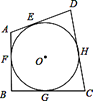 A、1 B、2 C、3 D、46. 以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD周长之比为( )
A、1 B、2 C、3 D、46. 以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD周长之比为( ) A、4:5 B、5:6 C、6:7 D、7:87. 如图,PA,PB分别切⊙O于点A,B,AC是⊙O的直径,连结AB,BC,OP,则与∠PAB相等的 角(不包括∠PAB本身)有( )
A、4:5 B、5:6 C、6:7 D、7:87. 如图,PA,PB分别切⊙O于点A,B,AC是⊙O的直径,连结AB,BC,OP,则与∠PAB相等的 角(不包括∠PAB本身)有( )
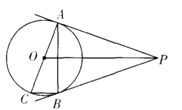 A、1个 B、2个 C、3个 D、4个8. 下列说法正确的是( )A、过任意一点总可以作圆的两条切线 B、圆的切线长就是圆的切线的长度 C、过圆外一点所画的圆的两条切线长相等 D、过圆外一点所画的圆的切线长一定大于圆的半径9. 如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm , 小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A、1个 B、2个 C、3个 D、4个8. 下列说法正确的是( )A、过任意一点总可以作圆的两条切线 B、圆的切线长就是圆的切线的长度 C、过圆外一点所画的圆的两条切线长相等 D、过圆外一点所画的圆的切线长一定大于圆的半径9. 如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm , 小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )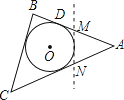 A、20cm B、15cm C、10cm D、随直线MN的变化而变化10.
A、20cm B、15cm C、10cm D、随直线MN的变化而变化10.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形的上底AD、下底BC以及腰AB均相切,切点分别是D、C、E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( ).
 A、9 B、10 C、12 D、14
A、9 B、10 C、12 D、14二、填空题
-
11. 如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为 .
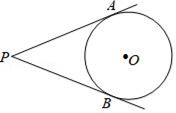
 12. 已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为 cm.13. 如图,从⊙O外一点P引圆的两条切线PA,PB,切点为A,B,点C是劣弧AB上一点,过C的切线交PA,PB于M,N.若⊙O的半径为2,∠P=60°,则△PMN的周长为.
12. 已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为 cm.13. 如图,从⊙O外一点P引圆的两条切线PA,PB,切点为A,B,点C是劣弧AB上一点,过C的切线交PA,PB于M,N.若⊙O的半径为2,∠P=60°,则△PMN的周长为. 14. 把直尺、三角尺和圆形螺母按如图所示放置于桌面上, ,若量出 ,则圆形螺母的外直径是 .
14. 把直尺、三角尺和圆形螺母按如图所示放置于桌面上, ,若量出 ,则圆形螺母的外直径是 .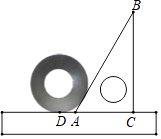 15. 如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为 .
15. 如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为 .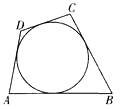 16. 如图,矩形ABCD中,AB=4,AD=8,点E,F分别在边AD,BC上,且点B,F关于过点E的直线对称,如果EF与以CD为直径的圆恰好相切,那么AE= .
16. 如图,矩形ABCD中,AB=4,AD=8,点E,F分别在边AD,BC上,且点B,F关于过点E的直线对称,如果EF与以CD为直径的圆恰好相切,那么AE= .
三、解答题
-
17. 如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.
 18. 如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,求⊙O的半径.
18. 如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,求⊙O的半径.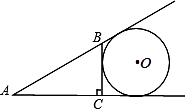 19. 如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2-mx+m-1=0的两个根,求△PCD的周长.
19. 如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2-mx+m-1=0的两个根,求△PCD的周长. 20. 如图,☉O与四边形ABCD的四边都相切.若∠AOB=70°,求∠COD的度数.
20. 如图,☉O与四边形ABCD的四边都相切.若∠AOB=70°,求∠COD的度数. 21. 如图, 是 的直径,过 外一点 作 的两条切线 , ,切点分别为 , ,连接 , .
21. 如图, 是 的直径,过 外一点 作 的两条切线 , ,切点分别为 , ,连接 , . (1)、求证: ;
(1)、求证: ;
(2)、连接 , ,若 , , ,求 的长.22. 如图,已知⊙O与等腰△ABD的两腰AB、AD分别相切于点E、F,连接AO并延长到点C,使OC=AO,连接CD、CB. (1)、试判断四边形ABCD的形状,并说明理由;(2)、若AB=4cm,填空:
(1)、试判断四边形ABCD的形状,并说明理由;(2)、若AB=4cm,填空:①当⊙O的半径为cm时,△ABD为等边三角形;
②当⊙O的半径为cm时,四边形ABCD为正方形.
23. 综合题
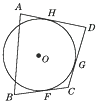
(1)、如图,四边形ABCD是☉O的外切四边形,切点分别为E,F,G,H,说明AB+CD与BC+AD的大小关系. (2)、如图,四边形ABCD的三边切☉O于F,G,H,说明AB+CD与BC+AD的大小关系.
(2)、如图,四边形ABCD的三边切☉O于F,G,H,说明AB+CD与BC+AD的大小关系. (3)、如图,四边形ABCD的三边切☉O于F,G,H,说明AB+CD与BC+AD的大小关系.
(3)、如图,四边形ABCD的三边切☉O于F,G,H,说明AB+CD与BC+AD的大小关系.