2018-2019学年初中数学北师大版九年级下册3.5确定圆的条件 同步练习
试卷更新日期:2019-03-13 类型:同步测试
一、单选题
-
1. 过A,B,C三点能确定一个圆的条件是( )
①AB=2,BC=3,AC=5;②AB=3, BC=3,AC=2;③AB=3,BC=4,AC= 5.
A、①② B、①②③ C、②③ D、①③2. 如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是( )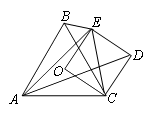 A、△CBE B、△ACD C、△ABE D、△ACE3. 对于三角形的外心,下列说法错误的是( )A、它到三角形三个顶点的距离相等 B、它是三角形外接圆的圆心 C、它是三角形三条边垂直平分线的交点 D、它一定在三角形的外部4. 如图,小明为检验四边形MNPQ四个顶点是否在同一圆上,用尺规分别作了MN,MQ的垂直平分线交于点O,则M,N,P,Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )
A、△CBE B、△ACD C、△ABE D、△ACE3. 对于三角形的外心,下列说法错误的是( )A、它到三角形三个顶点的距离相等 B、它是三角形外接圆的圆心 C、它是三角形三条边垂直平分线的交点 D、它一定在三角形的外部4. 如图,小明为检验四边形MNPQ四个顶点是否在同一圆上,用尺规分别作了MN,MQ的垂直平分线交于点O,则M,N,P,Q四点中,不一定在以O为圆心,OM为半径的圆上的点是( )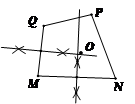 A、点M B、点N C、点P D、点Q5. 如图,点O是△ABC的内切圆的圆心,若∠A=80°,则∠BOC为( )
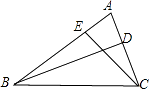
A、点M B、点N C、点P D、点Q5. 如图,点O是△ABC的内切圆的圆心,若∠A=80°,则∠BOC为( )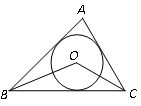 A、100° B、130° C、50° D、65°6. 在Rt△ABC中,∠C=90°,AC=6,BC=8,则这个三角形的外接圆的半径是( )A、10 B、5 C、4 D、37. 如图,已知 , , ,则 的度数为( )
A、100° B、130° C、50° D、65°6. 在Rt△ABC中,∠C=90°,AC=6,BC=8,则这个三角形的外接圆的半径是( )A、10 B、5 C、4 D、37. 如图,已知 , , ,则 的度数为( )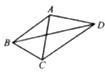 A、68° B、88° C、90° D、112°8. 如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是( )
A、68° B、88° C、90° D、112°8. 如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是( ) A、△CBE B、△ACD C、△ABE D、△ACE9. 在Rt△ABC中,两直角边AC=6cm,BC=8cm,则它的外接圆的面积为( )A、100πcm² B、15πcm² C、25πcm² D、50πcm²10. 正三角形的外接圆的半径和高的比为( )A、1∶2 B、2∶3 C、3∶4 D、1∶3
A、△CBE B、△ACD C、△ABE D、△ACE9. 在Rt△ABC中,两直角边AC=6cm,BC=8cm,则它的外接圆的面积为( )A、100πcm² B、15πcm² C、25πcm² D、50πcm²10. 正三角形的外接圆的半径和高的比为( )A、1∶2 B、2∶3 C、3∶4 D、1∶3二、填空题
-
11. 两直角边长分别为6和8的直角三角形的外接圆直径是 .
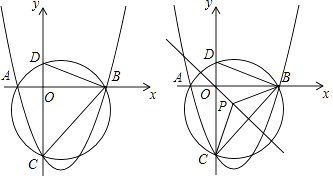
12. 已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是(填“锐角三角形”或“直角三角形”或“钝角三角形”).13. 如图,△ABC的外接圆的圆心坐标为 . 14. 锐角三角形的外心在 , 直角三角形的外心在 ,钝角三角形的外心在.
14. 锐角三角形的外心在 , 直角三角形的外心在 ,钝角三角形的外心在.
15. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为 . 16. 如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
16. 如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .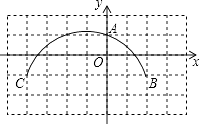
三、综合题
-
17. 考古学家发现了一块古代圆形陶器残片如图所示,为了修复这块陶器残片,需要找出圆心.
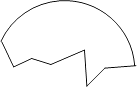 (1)、请利用尺规作图确定这块残片的圆心O;(保留作图痕迹,不写作法)
(1)、请利用尺规作图确定这块残片的圆心O;(保留作图痕迹,不写作法)
(2)、写出作图的主要依据:18. 如图,在等腰直角△ABC中,∠ACB=90°,AC=BC= . (1)、作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法).(2)、在(1)所作的圆中,圆心角∠BOC=º,圆的半径为,劣弧 的长为.19. 如图,已知线段AB.
(1)、作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法).(2)、在(1)所作的圆中,圆心角∠BOC=º,圆的半径为,劣弧 的长为.19. 如图,已知线段AB. (1)、仅用没有刻度的直尺和圆规作一个以AB为腰、底角等于30°的等腰△ABC.(保留作图痕迹,不要求写作法)
(1)、仅用没有刻度的直尺和圆规作一个以AB为腰、底角等于30°的等腰△ABC.(保留作图痕迹,不要求写作法)
(2)、在(1)的前提下,若AB=2cm,则等腰△ABC的外接圆的半径为 cm.20. 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.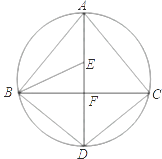 (1)、求证:BD=CD;(2)、请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.21. “不在同一直线上的三点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.
(1)、求证:BD=CD;(2)、请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.21. “不在同一直线上的三点确定一个圆”.请你判断平面直角坐标系内的三个点A(2,3),B(-3,-7),C(5,11)是否可以确定一个圆.
22. 如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.