2018-2019学年初中数学北师大版九年级下册3.4圆周角和圆心角的关系 同步练习
试卷更新日期：2019-03-13 类型：同步测试
一、单选题
-
1. 如图， ， ， 是 上的三点，且 ，则 的度数是（ ）
A、 B、 C、 D、 或2. 如图，边长为1的小正方形构成的网格中，半径为1的⊙O的圆心O在格点上，则∠BED的正切值等于（ ）
A、 B、 C、2 D、3. 如图，△ABC内接于⊙O，连结OA，OB，∠ABO=40。则∠C的度数是（ ）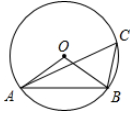
A、100° B、80° C、50° D、40°4. AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上。斜边过点B．一条直角边交该半圆于点Q．若AB=2，则线段BQ的长为（ ）
A、 B、 C、 D、5. 如图，▱ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，连接AE ， ∠E=55°，则∠ADC的度数是（ ）
A、55° B、45° C、35° D、25°6. 下列说法正确的是（ ）A、同圆或等圆中弧相等，则它们所对的圆心角也相等 B、0°的圆心角所对的弦是直径 C、平分弦的直径垂直于这条弦 D、三点确定一个圆7. 四边形ABCD内接于⊙O，则∠A∶∠B∶∠C∶∠D的值可以是（ ）
A、2∶3∶4∶5 B、2∶4∶3∶5 C、2∶5∶3∶4 D、2∶3∶5∶48. 如图，在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连结CD．若点D与圆心O不重合，∠BAC=26°，则∠DCA的度数为（ ）
A、36° B、38° C、40° D、42°9. 如图， 是 的直径， 是弦， ，垂足为点 ，连接 、 、 ， ， ，那么 的长为（ ）
A、 B、 C、 D、10. 如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，则下列说法中正确的有（ ）①点C、O、B一定在一条直线上；②若点E、点D分别是CA、AB的中点，则OE=OD；③若点E是CA的中点，连接CO，则△CEO是等腰直角三角形．
A、3个 B、2个 C、0个二、填空题
-
11. 如图，△ABC内接于圆O，若∠A=m° ，则∠OBC=度(用含m的代数式表示)
12. 如图等腰三角形△ABC的底角∠C为70°， 以腰AB为直径作半圆，交BC于点D，交AC于点E，则 的度数为
13. 如图，在△ABC中，AB=AC=10，以AB为直径的⊙O与BC交于点D，与AC交于点E，连接OD，交BE于点M且MD=2， 则BE长为.
14. 如图，△ABC内接于⊙O，连接OB、OC，若∠BAC=72°，则∠OCB的度数为 ．
15. 如图，四边形ABCD内接于⊙O，E为直径CD延长线上一点，且AB∥CD，若∠C=70°，则∠ADE的大小为 ．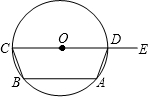
16. 如图，量角器的直径与直角三角尺ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转，CP与量角器的半圆弧交于点E，则第20秒点E在量角器上对应的读数是°．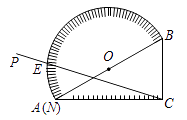
三、解答题
-
17. 已知：如图△ABC内接于圆O，AB=AC，D为弧BC上任意一点，连结AD，BD
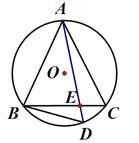(1)、若∠ADB=65°，求∠BAC的度数(2)、求证：∠ABD=∠AEB18. 已知：如图，AB是⊙O的直径，弦CD⊥AB于点E，G是 上一动点，AG，DC的延长线交于点F，连结BC．
(1)、若AB=4，∠B=60°，求 的长；(2)、设∠DGF= °，∠BCD= °，求 关于 的函数表达式．19. 如图，四边形ABCD内接于⊙O，AC平分∠BAD，延长DC交AB的延长线于点E．
(1)、若∠ADC=86°，求∠CBE的度数；(2)、若AC=EC，求证：AD=BE20. 已知△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E(1)、当∠BAC为锐角时，如图①，求证：∠CBE= ∠BAC
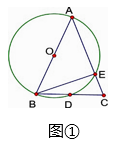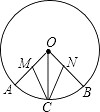
(2)、当∠BAC为钝角时，如图②，CA的延长线与⊙O相交于点E，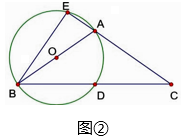
21. 如图，已知OA、OB、OC是⊙O的三条半径，点C是弧AB的中点，M、N分别是OA、OB的中点．求证：MC=NC．
