2018-2019学年初中数学北师大版九年级下册3.3垂径定理 同步练习
试卷更新日期:2019-03-13 类型:同步测试
一、单选题
-
1. 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
 A、 B、 C、1 D、22. 如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )
A、 B、 C、1 D、22. 如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )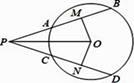 A、1 B、2 C、3 D、43. 已知点E在半径为5的⊙O上运动,AB是⊙O的弦且AB=8,则使△ABE的面积为8 的点E共有( )个
A、1 B、2 C、3 D、43. 已知点E在半径为5的⊙O上运动,AB是⊙O的弦且AB=8,则使△ABE的面积为8 的点E共有( )个
A、 1 B、2 C、3 D、44. 下列命题正确的个数是( )①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.
A、1个 B、2个 C、3个 D、4个5. 如图,在平面直角坐标系中,⊙P的圆心是( , a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为2 ,则a的值是( ) A、2
A、2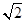 B、2+
B、2+ 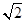 C、2
D、2+
6. 如图 ,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移 ,如图 , 边与圆的两个交点对应 的长为 ,则可知井盖的直径是( )
C、2
D、2+
6. 如图 ,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移 ,如图 , 边与圆的两个交点对应 的长为 ,则可知井盖的直径是( ) A、25cm B、30cm C、50cm D、60cm7. 在半径为5 cm的⊙O中,弦AB的长为6 cm,当弦AB的两个端点A,B在⊙O上滑动时,AB的中点在滑动过程中所经过的路线为( )
A、25cm B、30cm C、50cm D、60cm7. 在半径为5 cm的⊙O中,弦AB的长为6 cm,当弦AB的两个端点A,B在⊙O上滑动时,AB的中点在滑动过程中所经过的路线为( )
A、正方形 B、直线 C、圆 D、多边形8. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( ) A、10 cm B、10cm C、10 cm D、8 cm9. 如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,过点C作⊙O切线交OE的延长线于点F,已知BC=8,DE=2,则⊙O的半径为( )
A、10 cm B、10cm C、10 cm D、8 cm9. 如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,过点C作⊙O切线交OE的延长线于点F,已知BC=8,DE=2,则⊙O的半径为( )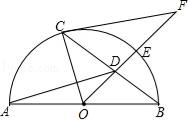 A、8 B、5 C、2.5 D、610. 《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
A、8 B、5 C、2.5 D、610. 《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”如图所示,请根据所学知识计算:圆形木材的直径AC是( )
 A、13寸 B、20寸 C、26寸 D、28寸
A、13寸 B、20寸 C、26寸 D、28寸二、填空题
-
11. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为 .
12. 如图,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .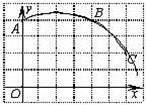 13. 如图,某种鱼缸的主视图可视为弓形,该鱼缸装满水时的最大深度CD为18cm,半径OC为13cm,则鱼缸口的直径AB= cm.
13. 如图,某种鱼缸的主视图可视为弓形,该鱼缸装满水时的最大深度CD为18cm,半径OC为13cm,则鱼缸口的直径AB= cm.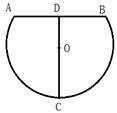 14. 如图,A(1,0)、B(3,0),以AB为直径作⊙M,射线OF交⊙M于E、F两点,C为弧AB 的中点,D为EF的中点.当射线OF绕O点旋转时,CD的最小值为.
14. 如图,A(1,0)、B(3,0),以AB为直径作⊙M,射线OF交⊙M于E、F两点,C为弧AB 的中点,D为EF的中点.当射线OF绕O点旋转时,CD的最小值为.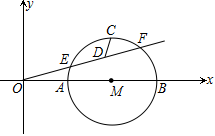 15. 点P是半径为5的⊙O内点,OP=3,在过点P的所有弦中,弦长为整数的弦的条数为条。16. 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为;点E在运动过程中,线段FG的长度的最小值为 .
15. 点P是半径为5的⊙O内点,OP=3,在过点P的所有弦中,弦长为整数的弦的条数为条。16. 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为;点E在运动过程中,线段FG的长度的最小值为 .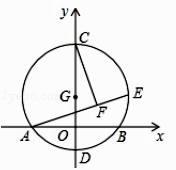
三、解答题
-
17. 如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
 18. 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图所示).
18. 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图所示). (1)、求证:AC=BD;
(1)、求证:AC=BD;
(2)、若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长
19. 如图,已知AB、CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F,OE=OF,求证:AB=CD.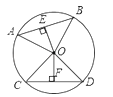 20. 用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.
20. 用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径. 21. 如图,一条公路的转弯处是一段圆弧
21. 如图,一条公路的转弯处是一段圆弧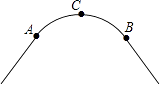 (1)、用直尺和圆规作出 所在圆的圆心O; 要求保留作图痕迹,不写作法(2)、若 的中点C到弦AB的距离为 ,求 所在圆的半径.22. 如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)、用直尺和圆规作出 所在圆的圆心O; 要求保留作图痕迹,不写作法(2)、若 的中点C到弦AB的距离为 ,求 所在圆的半径.22. 如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.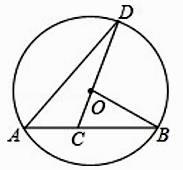 (1)、弦长AB等于(结果保留根号);(2)、当∠D=20°时,求∠BOD的度数.23. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
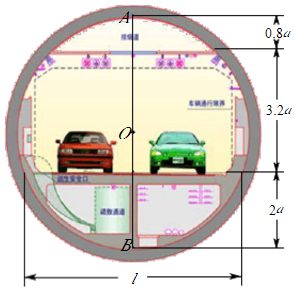
(1)、弦长AB等于(结果保留根号);(2)、当∠D=20°时,求∠BOD的度数.23. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面. (1)、请你补全这个输水管道的圆形截面;(2)、若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.24. 生活中看似平常的隧道设计也很精巧.如图是一张盾构隧道断面结构图,隧道内部为以O为圆心AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为0.8a,顶棚到路面的距离是3.2a,点B到路面的距离为2a.请你求出路面的宽度l.(用含a的式子表示)
(1)、请你补全这个输水管道的圆形截面;(2)、若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.24. 生活中看似平常的隧道设计也很精巧.如图是一张盾构隧道断面结构图,隧道内部为以O为圆心AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为0.8a,顶棚到路面的距离是3.2a,点B到路面的距离为2a.请你求出路面的宽度l.(用含a的式子表示)