2018-2019学年初中数学北师大版九年级下册3.2圆的对称性 同步练习
试卷更新日期：2019-03-13 类型：同步测试
一、单选题
-
1. 如果两条弦相等，那么（ ）A、这两条弦所对的圆心角相等 B、这两条弦所对的弧相等 C、这两条弦所对的弦心距相等 D、以上说法都不对2. 如图，A，B，C，D是⊙O上的四个点，AD∥BC．那么 与 的数量关系是（ ）
A、 = B、 ＞ C、 ＜ D、无法确定3. 如图，△ABC内接于半径为5的⊙O，点B在⊙O上，cosB= ，则下列量中，值会发生变化的量是（ ）
A、∠B的度数 B、BC的长 C、AC的长 D、的长4. 如图，AB是半圆O的直径，点C在半圆O上，把半圆沿弦AC折叠，AC恰好经过点O，则BC与AC的关系是（ ）
A、弧BC= 弧AC B、弧BC= 弧AC C、弧BC=弧AC D、不能确定5. 如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=10，AE=2，则弦CD的长是（ ）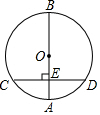
A、4 B、6 C、8 D、106. 以下命题：①直径相等的圆是等圆；②长度相等弧是等弧；③相等的弦所对的弧也相等；④圆的对称轴是直径；其中正确的个数是（ ）A、4 B、3 C、2 D、17. 如图， ， ， 是 的三等分点， 分别交 ， 于点 ， ，则下列结论正确的个数有（ ）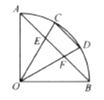
① ； ② ；
③ ； ④ .
A、1个 B、2个 C、3个 D、4个8. 已知AB，CD是两个不同圆的弦，如AB=CD，那么与的关系是（ ）
A、AB=CD B、AB>CD C、AB<CD D、不能确定9. 把一张圆纸片按如图所示方式折叠两次后展开，图中的虚线表示折痕，则弧AB的度数是（ ）
A、120° B、135° C、150° D、165°10. 如图，AB是⊙O的直径， = = ，∠COD=34°，则∠AEO的度数是（ ）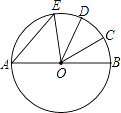
A、51° B、56° C、68° D、78°二、填空题
-
11. 如图，点A、B把⊙O分成 两条弧，则∠AOB= ．
12. 如图，AB是⊙O的直径，C、D为半圆的三等分点，CE⊥AB于点E，∠ACE的度数为 ．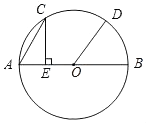
13. 如图，在⊙O中，C，D分别是OA，OB的中点，MC⊥AB，ND⊥AB，M，N在⊙O上．下列结论：①MC＝ND；② ；③四边形MCDN是正方形；④MN＝ AB，其中正确的结论是(填序号)．
14. 如图，圆心角∠AOB＝20°，将 旋转n°得到 ，则 的度数是度．
15. 如图，AB是⊙O的直径，点C在⊙O上，∠AOC=40°，D是BC弧的中点，则∠ACD= ．
16. 如图，已知AB是⊙O的直径，C、D、E、F、G是 上的点，且有 ，则∠OCG= ．
三、解答题
-
17. 已知：如图，A，B，C，D是⊙O上的点，且AB=CD，求证：∠AOC=∠BOD．
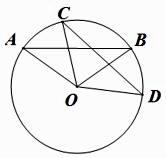18. 已知，如图，AD=BC.求证：AB=CD
. 19. 如图： ，D、E分别是半径OA和OB的中点，求证：CD=CE．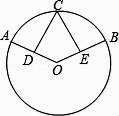
20. 如图，CD为⊙O直径，以C点为圆心，CO为半径作弧，交⊙O于A、B两点，求证：AD=BD=BA．
21. 如图，AB，CD，EF都是☉O的直径，且∠1=∠2=∠3，求证：AC=EB=DF.
22. 如图，⊙O的两条弦AB、CD交于点E，OE平分∠BED．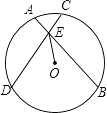
(1)、求证：AB=CD；(2)、若∠BED=60°，EO=2，求DE﹣AE的值．23. 如图， 的半径为5，弦 于E， ．
(1)、求证： ；(2)、若 于F， 于G，试说明四边形OFEG是正方形．24. 我们学习了“圆心角、弧、弦的关系”，实际上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”如下：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距(弦心距指从圆心到弦的距离，如图1中的OC、OC′，弦心距也可以说成圆心到弦的垂线段的长度)中有一组量相等，那么它们对应的其余各组量也相等．请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题：如图2，O是∠EPF的平分线上一点，以点O为圆心的圆与角的两边分别交于点A、B、C、D．
(1)、求证：AB＝CD；(2)、若角的顶点P在圆上，上述结论还成立吗？若不成立，请说明理由；若成立，请加以证明．