2018-2019学年初中数学北师大版九年级下册2.5二次函数与一元二次方程 同步练习
试卷更新日期:2019-03-13 类型:同步测试
一、单选题
-
1. 抛物线 与 轴的交点坐标是( )A、(0, 1) B、(1, 0) C、(0, -1) D、(0, 0)2. 如图为抛物线y=ax2+bx+c的图象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
 A、a+b=﹣1 B、a﹣b=﹣1 C、b<2a D、ac<03. 二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x的四组对应值如表所示
A、a+b=﹣1 B、a﹣b=﹣1 C、b<2a D、ac<03. 二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x的四组对应值如表所示x
6.15
6.18
6.21
6.24
y
0.02
-0.01
0.02
0.11
则方程ax2+bx+c=0的根的个数是( )
A、0 B、1 C、2 D、不能确定4. 小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( ) A、无解 B、x=1 C、x=﹣4 D、x=﹣1或x=45. 已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2014的值为( )A、2012 B、2013 C、2014 D、20156. 如图,抛物线 与x轴交于点A、B,把抛物线在x轴及其下方的部分记作 ,将 向左平移得到 , 与x轴交于点B、D,若直线 与 、 共有3个不同的交点,则m的取值范围是
A、无解 B、x=1 C、x=﹣4 D、x=﹣1或x=45. 已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2014的值为( )A、2012 B、2013 C、2014 D、20156. 如图,抛物线 与x轴交于点A、B,把抛物线在x轴及其下方的部分记作 ,将 向左平移得到 , 与x轴交于点B、D,若直线 与 、 共有3个不同的交点,则m的取值范围是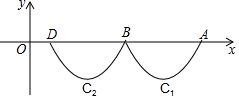 A、
A、 B、
B、 C、
C、 D、
D、 7. 下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,下确的是( )
7. 下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,下确的是( )
A、没有交点 B、只有一个交点,且它位于y轴右侧 C、有两个交点,且它们均位于y轴左侧 D、有两个交点,且它们均位于y轴右侧8. 二次函数y=x2+2x﹣m2+1的图像与直线y=1的公共点个数是( )A、0 B、1 C、2 D、1或29. 根据抛物线y=x2+3x-1与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )
A、x2+3x-1=0 B、x2+3x+1=0 C、3x2+x-1=0 D、x2-3x+1=010. “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A、 B、 C、 D、二、填空题
-
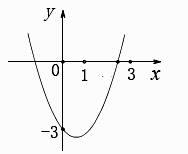
11. 二次函数 与两坐标轴的三个交点确定的三角形的面积是 .12. 如图,已知抛物线y=x2+bx+c经过点(0,-3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值是 .
 13. 若抛物线y=2 +x+c与坐标轴有两个交点,则字母c应满足的条件是 .14. 若函数 的图像与x轴有且只有一个交点,则a的值为 .
13. 若抛物线y=2 +x+c与坐标轴有两个交点,则字母c应满足的条件是 .14. 若函数 的图像与x轴有且只有一个交点,则a的值为 .
15. 二次函数y=ax2+bx+c的图象如图所示,则方程ax2+bx+c=0的两根为 . 16. 二次函数y=x2+ax+a与x轴的交点分别是A(x1 , 0)、B(x2 , 0),且x1+x2-x1x2=-10,则抛物线的顶点坐标是 .
16. 二次函数y=x2+ax+a与x轴的交点分别是A(x1 , 0)、B(x2 , 0),且x1+x2-x1x2=-10,则抛物线的顶点坐标是 .
三、解答题
-
17. 如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
 (1)、求抛物线的解析式及顶点D的坐标;(2)、在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为 .
(1)、求抛物线的解析式及顶点D的坐标;(2)、在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为 .(注:抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣ ,顶点坐标为(﹣ , )
18. 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.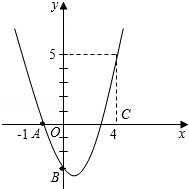 (1)、观察图象,写出A、B、C三点的坐标,并求出抛物线解析式;(2)、求此抛物线的顶点坐标和对称轴;(3)、当m取何值时,ax2+bx+c=m有两个不相等的实数根.19. 已知一元二次方程x2+x﹣2=0有两个不相等的实数根,即x1=1,x2=﹣2.(1)、求二次函数y=x2+x﹣2与x轴的交点坐标;(2)、若二次函数y=﹣x2+x+a与x轴有一个交点,求a的值.
(1)、观察图象,写出A、B、C三点的坐标,并求出抛物线解析式;(2)、求此抛物线的顶点坐标和对称轴;(3)、当m取何值时,ax2+bx+c=m有两个不相等的实数根.19. 已知一元二次方程x2+x﹣2=0有两个不相等的实数根,即x1=1,x2=﹣2.(1)、求二次函数y=x2+x﹣2与x轴的交点坐标;(2)、若二次函数y=﹣x2+x+a与x轴有一个交点,求a的值.
20. 已知:二次函数y=﹣2x2+4x+m+1,与x轴的公共点为A,B. (1)、如果A与B重合,求m的值;(2)、横、纵坐标都是整数的点叫做整点:
(1)、如果A与B重合,求m的值;(2)、横、纵坐标都是整数的点叫做整点:①当m=﹣1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n≤8时,结合函数的图象,求m的取值范围.
21. 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x-1)2-4,AB为半圆的直径,求这个“果圆”被y轴截得的CD的长. 22. 已知二次函数 ( 为常数).(1)、求证:不论 为何值,该函数的图象与 轴总有公共点;(2)、当 取什么值时,该函数的图象与 轴的交点在 轴的上方?
22. 已知二次函数 ( 为常数).(1)、求证:不论 为何值,该函数的图象与 轴总有公共点;(2)、当 取什么值时,该函数的图象与 轴的交点在 轴的上方?
23. 根据下列要求,解答相关问题. (1)、请补全以下求不等式 的解集的过程:
(1)、请补全以下求不等式 的解集的过程:①构造函数,画出图象:根据不等式特征构造二次函数y= ;并在下面的坐标系中(图1)画出二次函数y= 的图象(只画出大致图象即可);
②求得界点,标示所需:当 时,求得方程 的解为;并用虚线标示出函数y= 图象中 <0的部分;
③借助图象,写出解集:由所标示图象,可得不等式 <0的解集为.
(2)、请你利用上面求不等式解集的过程,求不等式 -3≥0的解集.
24. 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:t(秒)
0
0.16
0.2
0.4
0.6
0.64
0.8
6
X(米)
0
0.4
0.5
1
1.5
1.6
2
…
y(米)
0.25
0.378
0.4
0.45
0.4
0.378
0.25
…
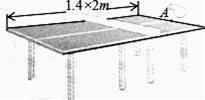 (1)、当t为何值时,乒乓球达到最大高度?(2)、乒乓球落在桌面时,与端点A的水平距离是多少?(3)、乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.
(1)、当t为何值时,乒乓球达到最大高度?(2)、乒乓球落在桌面时,与端点A的水平距离是多少?(3)、乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求a的值.