2016年广西河池市中考数学试卷
试卷更新日期:2017-04-25 类型:中考真卷
一、选择题
-
1. 下列各数中,比﹣1小的数是( )A、﹣2 B、0 C、1 D、22. 如图,AB∥CD,∠1=50°,则∠2的大小是( )
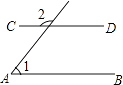 A、50° B、120° C、130° D、150°3. 下列四个几何体中,主视图为圆的是( )A、
A、50° B、120° C、130° D、150°3. 下列四个几何体中,主视图为圆的是( )A、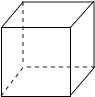 B、
B、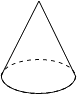 C、
C、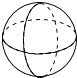 D、
D、 4. 下列长度的三条线段不能组成三角形的是( )A、5,5,10 B、4,5,6 C、4,4,4 D、3,4,55. 下列运算正确的是( )A、2a+3b=5ab B、2(2a﹣b)=4a﹣2b C、(a2)3=a5 D、a6÷a2=a36. 如图,不等式组 的解集在数轴上表示正确的是( )A、
4. 下列长度的三条线段不能组成三角形的是( )A、5,5,10 B、4,5,6 C、4,4,4 D、3,4,55. 下列运算正确的是( )A、2a+3b=5ab B、2(2a﹣b)=4a﹣2b C、(a2)3=a5 D、a6÷a2=a36. 如图,不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、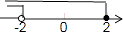 D、
D、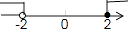 7. 要调查河池市中学生了解禁毒知识的情况,下列调查方式最适合的是( )A、在某中学抽取200名女生 B、在某中学抽取200名男生 C、在某中学抽取200名学生 D、在河池市中学生中随机抽取200名学生8. 如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
7. 要调查河池市中学生了解禁毒知识的情况,下列调查方式最适合的是( )A、在某中学抽取200名女生 B、在某中学抽取200名男生 C、在某中学抽取200名学生 D、在河池市中学生中随机抽取200名学生8. 如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( ) A、150° B、130° C、120° D、100°9. 二次函数y=ax2+bx+c的图象如图所示,则下列结论不正确的是( )
A、150° B、130° C、120° D、100°9. 二次函数y=ax2+bx+c的图象如图所示,则下列结论不正确的是( )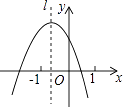 A、a<0 B、c>0 C、a+b+c>0 D、b2﹣4ac>010.
A、a<0 B、c>0 C、a+b+c>0 D、b2﹣4ac>010.如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(1, ),将线段OA绕原点O逆时针旋转30°,得到线段OB,则点B的坐标是( )
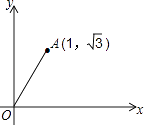 A、(0,2) B、(2,0) C、(1,﹣ ) D、(﹣1, )11. 如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A、(0,2) B、(2,0) C、(1,﹣ ) D、(﹣1, )11. 如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( ) A、AB=BC B、AC=BC C、∠B=60° D、∠ACB=60°12. 如图,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于A(0,2),B(0,8),则圆心P的坐标是( )
A、AB=BC B、AC=BC C、∠B=60° D、∠ACB=60°12. 如图,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于A(0,2),B(0,8),则圆心P的坐标是( ) A、(5,3) B、(5,4) C、(3,5) D、(4,5)
A、(5,3) B、(5,4) C、(3,5) D、(4,5)二、填空题
-
13. 代数式 在实数范围内有意义,则x的取值范围是 .14. 已知关于x的方程x2﹣3x+m=0的一个根是1,则m= .15. 同时抛掷两枚质地均匀的硬币,则两枚硬币全部正面向上的概率是 .16. 如图,AB是⊙O的直径,点C,D都在⊙O上,∠ABC=50°,则∠BDC的大小是 .
 17. 对于实数a,b,定义运算“*”:a*b= ,例如:因为4>2,所以4*2=42﹣4×2=8,则(﹣3)*(﹣2)= .18. 如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为 cm.
17. 对于实数a,b,定义运算“*”:a*b= ,例如:因为4>2,所以4*2=42﹣4×2=8,则(﹣3)*(﹣2)= .18. 如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为 cm.
三、解答题
-
19. 计算:|﹣1|﹣ tan45°+ ﹣30 .20. 先化简,再求值: •(x2﹣9)﹣3x,其中x=2.21. 如图,AE∥BF,AC平分∠BAE,交BF于C.
 (1)、尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);(2)、在(1)的图形中,找出两条相等的线段,并予以证明.22. 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y= (k≠0)的图象交于A(﹣3,2),B(2,n).
(1)、尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);(2)、在(1)的图形中,找出两条相等的线段,并予以证明.22. 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y= (k≠0)的图象交于A(﹣3,2),B(2,n). (1)、求反比例函数y= 的解析式;(2)、求一次函数y=ax+b的解析式;(3)、观察图象,直接写出不等式ax+b< 的解集.23. 某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整).
(1)、求反比例函数y= 的解析式;(2)、求一次函数y=ax+b的解析式;(3)、观察图象,直接写出不等式ax+b< 的解集.23. 某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整).
分数(分)
人数(人)
68
4
78
7
80
3
88
5
90
10
96
6
100
5
(1)、补全条形统计图;(2)、该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;(3)、该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?(4)、小明的成绩为88分,他的成绩如何,为什么?24. 某校需购买一批课桌椅供学生使用,已知A型课桌椅230元/套,B型课桌椅200元/套.(1)、该校购买了A,B型课桌椅共250套,付款53000元,求A,B型课桌椅各买了多少套?(2)、因学生人数增加,该校需再购买100套A,B型课桌椅,现只有资金22000元,最多能购买A型课桌椅多少套?25. 如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 的中点,连接CE,BE,BE交AC于F. (1)、求证:AB=AF;(2)、若AB=3,BC=4,求CE的长.26.
(1)、求证:AB=AF;(2)、若AB=3,BC=4,求CE的长.26.在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
 (1)、请直接写出点A,C,D的坐标;(2)、如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;(3)、如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
(1)、请直接写出点A,C,D的坐标;(2)、如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;(3)、如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.