2015-2016学年湖北省随州市随县七年级下学期期末数学试卷

试卷更新日期：2017-04-25 类型：期末考试

进入出卷网下载

一、选择题

1. 下列调查中，适宜采用全面调查（普查）方式的是（）

A、调查市场上老酸奶的质量情况 B、调查某品牌圆珠笔芯的使用寿命 C、调查乘坐飞机的旅客是否携带了危禁物品 D、调查我市市民对伦敦奥运会吉祥物的知晓率

查看试题解析
2. 如图，数轴上表示某不等式组的解集，则这个不等式组可能是（）

A、 ${\begin{matrix} x + 1 \geq 0 \\ 2 - x \geq 0 \end{matrix}$ B、 ${\begin{matrix} x + 1 \leq 0 \\ 2 - x \geq 0 \end{matrix}$ C、 ${\begin{matrix} x + 1 \leq 0 \\ x - 2 \geq 0 \end{matrix}$ D、 ${\begin{matrix} x + 1 \geq 0 \\ x - 2 \geq 0 \end{matrix}$

查看试题解析
3. 如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（）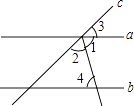

A、40° B、50° C、70° D、80°

查看试题解析
4. 在平面坐标系内，点A位于第二象限，距离x轴1个单位长度，距离y轴4个单位长度，则点A的坐标为（）

A、（1，4） B、（﹣4，1） C、（﹣1，﹣4） D、（4，﹣1）

查看试题解析
5. 关于x的方程组 ${\begin{matrix} 3 x - y = m \\ x + m y = n \end{matrix}$ 的解是 ${\begin{matrix} x = 1 \\ y = 1 \end{matrix}$ ，则 $\sqrt{m^{2} - n}$ 的值是（）

A、5 B、3 C、2 D、1

查看试题解析
6. 甲仓库乙仓库共存粮450吨，现从甲仓库运出存粮的60%，从乙仓库运出存粮的40%．结果乙仓库所余的粮食比甲仓库所余的粮食多30吨．若设甲仓库原来存粮x吨，乙仓库原来存粮y吨，则有（）

A、 ${\begin{matrix} x + y = 450 \\ (1 - 60 %) x - (1 - 40 %) y = 30 \end{matrix}$ B、 ${\begin{matrix} x + y = 450 \\ 60 % x - 40 y % = 30 \end{matrix}$ C、 ${\begin{matrix} x + y = 450 \\ (1 - 40 %)y - (1 - 60 %) x = 30 \end{matrix}$ D、 ${\begin{matrix} x + y = 450 \\ 40 % x - 60 y % = 30 \end{matrix}$

查看试题解析
7.
如图，将三角形向右平移2个单位长度，再向上平移3个单位长度，则平移后三个顶点的坐标是（）

A、（1，7），（﹣2，2），（3，4） B、（1，7），（﹣2，2），（4，3） C、（1，7），（2，2），（3，4） D、（1，7），（2，﹣2），（3，3）

查看试题解析
8. 将一直角三角板与两边平行的纸条如图所示放置，下列结论：①∠1=∠2；②∠3=∠4；③∠2+∠4=90°；④∠4+∠5=180°，其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 实数a、b在数轴上的位置如图所示，且|a|＞|b|，则化简 $\sqrt{a^{2}} - | a + b |$ 的结果为（）

A、2a+b B、﹣2a+b C、b D、2a﹣b

查看试题解析
10. 关于x的不等式组 ${\begin{matrix} 3 x - 1 > 4 (x - 1) \\ x < m \end{matrix}$ 的解集为x＜3，那么m的取值范围为（）

A、m=3 B、m＞3 C、m＜3 D、m≥3

查看试题解析

二、填空题

11. 若点P（a，b）在第四象限，则点M（b﹣a，a﹣b）在第象限．

查看试题解析
12. 已知y=1+ $\sqrt{2 x - 1}$ + $\sqrt{1 - 2 x}$ ，则2x+3y的平方根为．

查看试题解析
13. 若方程组 ${\begin{matrix} x = y + 5 \\ 2 x - y = 5 \end{matrix}$ 的解满足方程x+y+a=0，则a的值为

查看试题解析
14. 如图，直线AB∥CD∥EF，且∠B=40°，∠C=125°，则∠CGB= ．

查看试题解析
15. 有学生若干人，住若干间宿舍，若每间住4人，则有20人无法安排住宿，若每间住8人，则最后有一间宿舍不满也不空，则学生人数为人．

查看试题解析
16. 如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=a°．则下列结论：①∠BOE= $\frac{1}{2}$ （180﹣a）°；②OF平分∠BOD；③∠POE=∠BOF；④∠POB=2∠DOF．其中正确结论（填编号）．

查看试题解析

三、解答题

17. 计算： $\sqrt{81}$ + $\sqrt[3]{{(- 4)}^{3}}$ + $\sqrt{5^{2} - 3^{2}}$ ．

查看试题解析
18. 解不等式组： ${\begin{matrix} 2 x - 1 > 5 \\ \frac{3 x + 1}{2} - 1 \geq x \end{matrix}$ ，并在数轴上表示出不等式组的解集．

查看试题解析
19. ${\begin{matrix} \frac{1}{3} x + \frac{2}{3} (y - 1) = 2 \\ 2 (x - 1) = y - 1 \end{matrix}$

查看试题解析
20.
如图，平面直角坐标系中，已知点A（﹣3，3），B（﹣5，1），C（﹣2，0），P（a，b）是△ABC的边AC上任意一点，△ABC经过平移后得到△A₁B₁C₁ ，点P的对应点为P₁（a+6，b﹣2）．

(1)、直接写出点C₁的坐标；

(2)、在图中画出△A₁B₁C₁；

(3)、求△AOA₁的面积．

查看试题解析
21. 如图，∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并证明你的结论．
解：∠C与∠AED相等，理由如下：
∵∠1+∠2=180°（已知），∠1+∠DFE=180°（邻补角定义）
∴∠2= ．（．），
∴AB∥EF（．）
∴∠3= ．（．）
又∠B=∠3（已知）
∴∠B= ．（等量代换）
∴DE∥BC（．）
∴∠C=∠AED（．）．

查看试题解析
22. 某校学生会准备调查七年级叙述参加“绘画类”、“书法类”、“乐器类”四类校本课程的人数，在全校进行随机抽样调查，并根据收集的数据绘制了如图两幅统计图（信息尚不完整），请根据图中提供的信息，解答下面的问题：

(1)、此次共调查了多少名同学？

(2)、将条形图补充完整，并计算扇形统计图中乐器部分的圆心角的度数；

(3)、如果该校共有1000名学生参加这4个课外兴趣小组，而每个教师最多只能辅导本组的25名学生，估计书法兴趣小组至少需要准备多少名教师？

查看试题解析
23. 如图，已知AD∥BC，∠1=∠2，求证：∠3+∠4=180°．

查看试题解析
24. 同庆中学为丰富学生的校园生活，准备从军跃体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元．

(1)、购买一个足球、一个篮球各需多少元？

(2)、根据同庆中学的实际情况，需从军跃体育用品商店一次性购买足球和篮球共96个，要求购买足球和篮球的总费用不超过5720元，这所中学最多可以购买多少个篮球？

查看试题解析
25.
如图1，在平面直角坐标系中，A（a，0），C（b，2），且满足 ${(a + 2)}^{2} + \sqrt{b - 2} = 0$ ，过C作CB⊥x轴于B．

(1)、求△ABC的面积．

(2)、若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．

(3)、在y轴上是否存在点P，使得△ABC和△ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．

查看试题解析