2018-2019学年初中数学北师大版九年级下册2.3确定二次函数的表达式 同步练习
试卷更新日期:2019-03-13 类型:同步测试
一、单选题
-
1. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
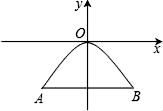 A、y= B、y=﹣ C、y=﹣ D、y=2. 二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
A、y= B、y=﹣ C、y=﹣ D、y=2. 二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:x
…
-5
-4
-3
-2
-1
0
…
y
…
4
0
-2
-2
0
4
…
下列说法正确的是( )
A、抛物线的开口向下 B、当 时,y随x的增大而增大
C、二次函数的最小值是
D、抛物线的对称轴是直线
时,y随x的增大而增大
C、二次函数的最小值是
D、抛物线的对称轴是直线 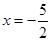 3. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
3. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )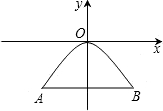 A、
A、 B、
B、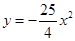 C、
C、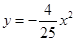 D、
D、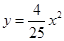 4. 若抛物线 与 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线 ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
4. 若抛物线 与 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线 ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A、 B、 C、 D、5. 平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如图所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为 ( )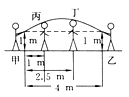 A、1.5 m B、1.625 m C、1.66 m D、1.67 m6. 太阳影子定位技术是通过分析视频中物体的太阳影子变化,确定视频拍摄地点的一种方法
A、1.5 m B、1.625 m C、1.66 m D、1.67 m6. 太阳影子定位技术是通过分析视频中物体的太阳影子变化,确定视频拍摄地点的一种方法 为了确定视频拍摄地的经度,我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻
为了确定视频拍摄地的经度,我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻  在一定条件下,直杆的太阳影子长度 单位:米 与时 单位:时 的关系满足函数关系 (a,b,c是常数),如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影子最短时,最接近的时刻t是( )
在一定条件下,直杆的太阳影子长度 单位:米 与时 单位:时 的关系满足函数关系 (a,b,c是常数),如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影子最短时,最接近的时刻t是( )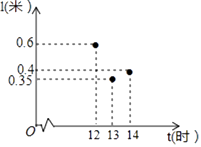 A、 B、13 C、 D、7. 若所求的二次函数图象与抛物线y=2x2-4x-1有相同的顶点,并且在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,则所求二次函数的表达式为( )A、y=-x2+2x+4 B、y=-ax2-2ax-3(a>0) C、y=-2x2-4x-5 D、y=ax2-2ax+a-3(a<0)8. 如图,老师出示了小黑板上的题后,小华添加的条件是过点(3,0);小彬添加的条件是过点(4,3);小明添加的条件是a=1;小颖添加的条件是抛物线被x轴截得的线段长为2.你认为四人添加的条件中,正确的有( )
A、 B、13 C、 D、7. 若所求的二次函数图象与抛物线y=2x2-4x-1有相同的顶点,并且在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,则所求二次函数的表达式为( )A、y=-x2+2x+4 B、y=-ax2-2ax-3(a>0) C、y=-2x2-4x-5 D、y=ax2-2ax+a-3(a<0)8. 如图,老师出示了小黑板上的题后,小华添加的条件是过点(3,0);小彬添加的条件是过点(4,3);小明添加的条件是a=1;小颖添加的条件是抛物线被x轴截得的线段长为2.你认为四人添加的条件中,正确的有( ) A、1个 B、2个 C、3个 D、4个9. 已知抛物线y=x2+bx+c(其中b,c是常数)经过点A(2,6),且抛物线的对称轴与线段BC有交点,其中点B(1,0),点C(3,0),则c的值不可能是( )
A、1个 B、2个 C、3个 D、4个9. 已知抛物线y=x2+bx+c(其中b,c是常数)经过点A(2,6),且抛物线的对称轴与线段BC有交点,其中点B(1,0),点C(3,0),则c的值不可能是( )
A、4 B、6 C、8 D、1010. 已知一条抛物线经过E(0,10),F(2,2),G(4,2),H(3,1)四点,选择其中两点用待定系数法能求出抛物线解析式的为( )A、E,F B、E,G C、E,H D、F,G11. 若二次函数y=x2+bx+5,配方后为y=(x﹣3)2+k,则b与k的值分别为( )A、﹣6,﹣4 B、﹣6,4 C、6,4 D、6,﹣412. 二次函数的图象如图所示,则这个二次函数的解析式为( )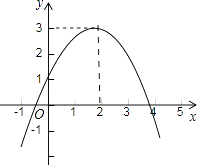 A、y (x﹣2)2+3 B、y= (x﹣2)2﹣3 C、y=﹣ (x﹣2)2+3 D、y=﹣ (x﹣2)2﹣313. 通过配方法将二次函数y=ax2+bx+c(a≠0)化成y=a(x﹣h)2+k的形式,此二次函数可变形为( )A、y=a(x+ )2+ B、y=a(x﹣ )2+ C、y=a(x+ )2+ D、y=a(x﹣ )2+14. 如果抛物线y=ax2+bx+c经过点(﹣1,12),(0,5)和(2,﹣3),则a+b+c的值为( )A、﹣4 B、﹣2 C、0 D、115. 已知一个二次函数,当x=1时,y有最大值8,其图象的形状、开口方向与抛物线y=﹣2x2相同,则这个二次函数的表达式是( )
A、y (x﹣2)2+3 B、y= (x﹣2)2﹣3 C、y=﹣ (x﹣2)2+3 D、y=﹣ (x﹣2)2﹣313. 通过配方法将二次函数y=ax2+bx+c(a≠0)化成y=a(x﹣h)2+k的形式,此二次函数可变形为( )A、y=a(x+ )2+ B、y=a(x﹣ )2+ C、y=a(x+ )2+ D、y=a(x﹣ )2+14. 如果抛物线y=ax2+bx+c经过点(﹣1,12),(0,5)和(2,﹣3),则a+b+c的值为( )A、﹣4 B、﹣2 C、0 D、115. 已知一个二次函数,当x=1时,y有最大值8,其图象的形状、开口方向与抛物线y=﹣2x2相同,则这个二次函数的表达式是( )
A、y=﹣2x2﹣x+3 B、y=﹣2x2+4 C、y=﹣2x2+4x+8 D、y=﹣2x2+4x+6二、填空题
-
16. 抛物线与x轴交于点(1,0),(﹣3,0),则该抛物线可设为: .17. 如图,已知抛物线 的对称轴为直线 ,且与 轴的一个交点为 ,那么它对应的函数解析式是 .
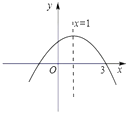 18. 已知关于x的二次函数y=3x2+2x+m+1的图象经过点(1,6),则m的值为.
18. 已知关于x的二次函数y=3x2+2x+m+1的图象经过点(1,6),则m的值为.
19. 请写出一个开口向上,且与y轴交于(0,-1)的二次函数的解析式 .20. 若抛物线 上有点 ,且当 时, 有最大值 ,则 , , .
21. 抛物线y=ax2+bx+c中,已知a:b:c=1:2:3,y最小值为6,则此抛物线的解析式为 .
三、解答题
-
22. 抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=a(x﹣3)2﹣1,且平移后的抛物线经过点A(2,1).
 (1)、求平移后抛物线的解析式;(2)、设原抛物线与y轴的交点为B,顶点为P,平移后抛物线的对称轴与x轴交于点M,求△BPM的面积.23. 如图,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).
(1)、求平移后抛物线的解析式;(2)、设原抛物线与y轴的交点为B,顶点为P,平移后抛物线的对称轴与x轴交于点M,求△BPM的面积.23. 如图,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).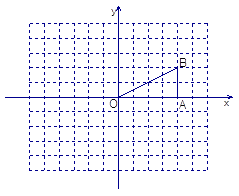 (1)、画出 关于点O成中心对称的 ,并写出点B1的坐标;
(1)、画出 关于点O成中心对称的 ,并写出点B1的坐标;
(2)、求出以点B1为顶点,并经过点B的二次函数关系式
24. 如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B在y轴上,点C(3,1),二次函数y= x2+bx﹣ 的图象经过点C.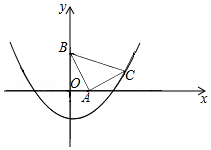 (1)、求二次函数的解析式,并把解析式化成y=a(x﹣h)2+k的形式;(2)、把△ABC沿x轴正方向平移,当点B落在抛物线上时,求△ABC扫过区域的面积;(3)、在抛物线上是否存在异于点C的点P,使△ABP是以AB为直角边的等腰直角三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.25. 如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=﹣ x2+bx+c经过B、D两点.
(1)、求二次函数的解析式,并把解析式化成y=a(x﹣h)2+k的形式;(2)、把△ABC沿x轴正方向平移,当点B落在抛物线上时,求△ABC扫过区域的面积;(3)、在抛物线上是否存在异于点C的点P,使△ABP是以AB为直角边的等腰直角三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.25. 如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=﹣ x2+bx+c经过B、D两点.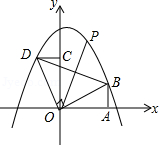 (1)、求二次函数的解析式;(2)、连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.26. 已知二次函数图象的顶点坐标为(1,4),且经过点(4,-5).(1)、求该二次函数表达式;(2)、直接写出y随x的增大而减小时x的取值范围;(3)、若二次函数的图象平移后经过原点,请直接写出两种不同的平移方案.27. 已知抛物线y=ax2+bx+c经过A(0,﹣5),B(1,﹣3),C(﹣1,11)三点,求抛物线的顶点坐标及对称轴.28. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)、求二次函数的解析式;(2)、连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.26. 已知二次函数图象的顶点坐标为(1,4),且经过点(4,-5).(1)、求该二次函数表达式;(2)、直接写出y随x的增大而减小时x的取值范围;(3)、若二次函数的图象平移后经过原点,请直接写出两种不同的平移方案.27. 已知抛物线y=ax2+bx+c经过A(0,﹣5),B(1,﹣3),C(﹣1,11)三点,求抛物线的顶点坐标及对称轴.28. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.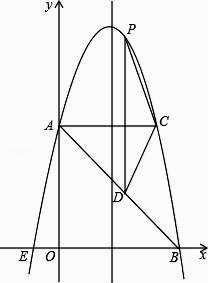 (1)、求二次函数y=ax2+bx+c的表达式;(2)、过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;(3)、若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.29. 如图1,已知抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,2),
(1)、求二次函数y=ax2+bx+c的表达式;(2)、过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;(3)、若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.29. 如图1,已知抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,2),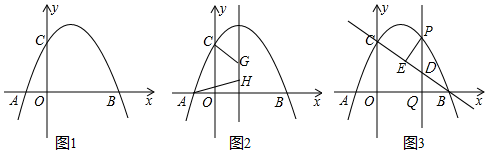 (1)、求抛物线的函数表达式;(2)、如图2,在抛物线对称轴上取两个点G、H(G在H的上方),且满足GH=1,连接CG,AH,求四边形CGHA的周长的最小值;(3)、如图3,点P是抛物线第一象限的一个动点,过点P作PQ⊥x轴于点Q,交BC于点D,PE⊥BC于点E,设△PDE的面积为S,求当S取得最大值时点P的坐标,并求S的最大值.
(1)、求抛物线的函数表达式;(2)、如图2,在抛物线对称轴上取两个点G、H(G在H的上方),且满足GH=1,连接CG,AH,求四边形CGHA的周长的最小值;(3)、如图3,点P是抛物线第一象限的一个动点,过点P作PQ⊥x轴于点Q,交BC于点D,PE⊥BC于点E,设△PDE的面积为S,求当S取得最大值时点P的坐标,并求S的最大值.