2018-2019学年初中数学北师大版九年级下册2.2二次函数的图像与性质 同步练习
试卷更新日期:2019-03-13 类型:同步测试
一、单选题
-
1. 由抛物线y=x2平移得到抛物线y=(x+2)2 , 下列平移方法可行的是( )A、向上平移2个单位长度 B、向下平移2个单位长度 C、向左平移2个单位长度 D、向右平移2个单位长度2. 已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为( )A、3或6 B、1或6 C、1或3 D、4或63. 如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为﹣1,则一次函数y=(a﹣b)x+b的图象大致是( )
 A、
A、 B、
B、 C、
C、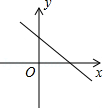 D、
D、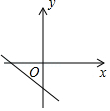 4. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a>0 ③b>0 ④c>0 ⑤9a+3b+c<0,则其中结论正确的个数是( )
4. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a>0 ③b>0 ④c>0 ⑤9a+3b+c<0,则其中结论正确的个数是( ) A、2个 B、3个 C、4个 D、5个5. 描点法画函数图象是研究陌生函数的基本方法.对于函数 ,下列说法:①图象经过 ;②当 时, 有最小值 ;③ 随 的增大而增大;④该函数图象关于直线 对称;正确的是( )
A、2个 B、3个 C、4个 D、5个5. 描点法画函数图象是研究陌生函数的基本方法.对于函数 ,下列说法:①图象经过 ;②当 时, 有最小值 ;③ 随 的增大而增大;④该函数图象关于直线 对称;正确的是( )
A、①② B、①②④ C、①②③④ D、②③④6. 已知抛物线 过 、 、 、 四点,则 与 的大小关系是( )
A、 > B、 = C、 < D、不能确定7. 把抛物线 向下平移 个单位长度,再向右平移 个单位长度,所得抛物线是( )
A、 B、 C、 D、8. 若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),则符合条件的点P( )A、有且只有1个 B、有且只有2个 C、至少有3个 D、有无穷多个9. 二次函数y=kx2+2x+1(k<0)的图象可能是( )A、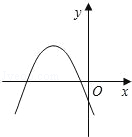 B、
B、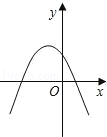 C、
C、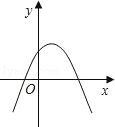 D、
D、 10. 如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )
10. 如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )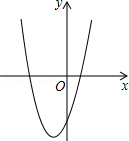 A、a>0,c>0 B、a<0,c>0 C、a>0,c<0 D、a<0,c<011. 函数y=ax2与函数y=ax+a,在同一直角坐标系中的图象大致是图中的( )A、
A、a>0,c>0 B、a<0,c>0 C、a>0,c<0 D、a<0,c<011. 函数y=ax2与函数y=ax+a,在同一直角坐标系中的图象大致是图中的( )A、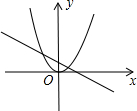 B、
B、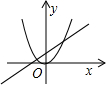 C、
C、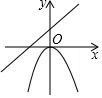 D、
D、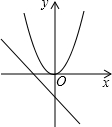 12. 下列二次函数的图象中,其对称轴是x=1的为( )A、
12. 下列二次函数的图象中,其对称轴是x=1的为( )A、 B、
B、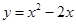 C、
C、 D、
D、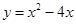 13. 当 时,二次函数 有最大值 ,则实数 的值为( )A、 B、 C、 D、2或 或14. 对于代数式 ,下列说法正确的是( )
13. 当 时,二次函数 有最大值 ,则实数 的值为( )A、 B、 C、 D、2或 或14. 对于代数式 ,下列说法正确的是( )①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则 ②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
A、① B、③ C、②④ D、①③15. 已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:x
-1
0
1
3
y
-3
1
3
1
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4,其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
16. 二次函数 的顶点坐标是 .
17. 将二次函数 的图象先向左平移 个单位长度,再向下平移 个单位长度,得到函数的图象的表达式是 .18. 已知抛物线y=x2+(m-4)x-4m的顶点在y轴上,则m=;19. 已知二次函数 有最大值 ,则 , 的大小关系为 .
20. 若二次函数 的图象关于 轴对称,则 的值为: . 此函数图象的顶点和它与 轴的两个交点所确定的三角形的面积为:.
21. 已知抛物线 的对称轴为直线 ,且经过点 , ,试比较 和 的大小: .(填“ ”,“ ”或“ ”)
三、解答题
-
22. 若二次函数y=﹣x2图象平移后得到二次函数y=﹣(x﹣2)2+4的图象.
 (1)、平移的规律是:先向(填“左”或“右”)平移个单位,再向平移个单位.(2)、在所给的坐标系内画出二次函数y=﹣(x﹣2)2+4的示意图.23. 已知抛物线y=-x2+2x+3.
(1)、平移的规律是:先向(填“左”或“右”)平移个单位,再向平移个单位.(2)、在所给的坐标系内画出二次函数y=﹣(x﹣2)2+4的示意图.23. 已知抛物线y=-x2+2x+3. (1)、求该抛物线的对称轴和顶点P的坐标.(2)、在图中的直角坐标系内用五点法画出该抛物线的图象(3)、将该抛物线向下平移2个单位,向左平移3个单位得到抛物线y1 , 此时点P的对应点为P′,试求直线PP′与y轴的交点坐标24. 已知二次函数y=x2+2x﹣3.(1)、写出它的顶点坐标;(2)、当x取何值时,y随x的增大而增大;(3)、求出图象与x轴的交点坐标.(4)、当x取何值时y的值大于0.25. 二次函数 的图象如图所示,根据图象回答:
(1)、求该抛物线的对称轴和顶点P的坐标.(2)、在图中的直角坐标系内用五点法画出该抛物线的图象(3)、将该抛物线向下平移2个单位,向左平移3个单位得到抛物线y1 , 此时点P的对应点为P′,试求直线PP′与y轴的交点坐标24. 已知二次函数y=x2+2x﹣3.(1)、写出它的顶点坐标;(2)、当x取何值时,y随x的增大而增大;(3)、求出图象与x轴的交点坐标.(4)、当x取何值时y的值大于0.25. 二次函数 的图象如图所示,根据图象回答: (1)、当 时,写出自变量 的值.(2)、当 时,写出自变量 的取值范围.(3)、写出 随 的增大而减小的自变量 的取值范围.
(1)、当 时,写出自变量 的值.(2)、当 时,写出自变量 的取值范围.(3)、写出 随 的增大而减小的自变量 的取值范围.
(4)、若方程 有两个不相等的实数根,求 的取值范围(用含 、 、 的代数式表示).26. 已知一条抛物线的开口方向和大小与抛物线y=3x2都相同,顶点与抛物线y=(x+2)2相同.
(1)、求这条抛物线的解析式;
(2)、将上面的抛物线向右平移4个单位会得到怎样的抛物线解析式?
(3)、若(2)中所求抛物线的顶点不动,将抛物线的开口反向,求符合此条件的抛物线解析式.27. 如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P. (1)、当抛物线F经过点C时,求它的表达式;(2)、设点P的纵坐标为yP , 求yP的最小值,此时抛物线F上有两点(x1 , y1),(x2 , y2),且x1<x2≤﹣2,比较y1与y2的大小;
(1)、当抛物线F经过点C时,求它的表达式;(2)、设点P的纵坐标为yP , 求yP的最小值,此时抛物线F上有两点(x1 , y1),(x2 , y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)、当抛物线F与线段AB有公共点时,直接写出m的取值范围.
28. 已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).(1)、求证无论k为何值,方程总有两个不相等实数根;(2)、已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;(3)、若原方程的一个根大于3,另一个根小于3,求k的最大整数值.29. 如图 ,若抛物线 的顶点 在抛物线 上,抛物线 的顶点 也在抛物线 上(点 与点 不重合),我们定义:这样的两条抛物 , 互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条. (1)、如图 ,已知抛物线 与 轴交于点 ,试求出点 关于该抛物线对称轴对称的点 的坐标;(2)、请求出以点 为顶点的 的友好抛物线 的解析式,并指出 与 中 同时随 增大而增大的自变量的取值范围;
(1)、如图 ,已知抛物线 与 轴交于点 ,试求出点 关于该抛物线对称轴对称的点 的坐标;(2)、请求出以点 为顶点的 的友好抛物线 的解析式,并指出 与 中 同时随 增大而增大的自变量的取值范围;
(3)、若抛物线 的任意一条友好抛物线的解析式为 ,请写出 与 的关系式,并说明理由.