2014年广西钦州市中考数学试卷
试卷更新日期:2017-04-25 类型:中考真卷
一、选择题
-
1. 如果收入80元记作+80元,那么支出20元记作( )A、+20元 B、﹣20元 C、+100元 D、﹣100元2. 一个几何体的三个视图如图所示,这个几何体是( )
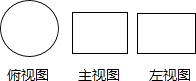 A、圆柱 B、球 C、圆锥 D、正方体3. 我市2014年参加中考的考生人数约为43400人,将43400用科学记数法表示为( )A、434×102 B、43.4×103 C、4.34×104 D、0.434×1054. 体育课上,两名同学分别进行了5次立定跳远测试,要判断这5次测试中谁的成绩比较稳定,通常需要比较这两名同学成绩的( )A、平均数 B、中位数 C、众数 D、方差5. 下列运算正确的是( )A、 = + B、( )2=3 C、3a﹣a=3 D、(a2)3=a56. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
A、圆柱 B、球 C、圆锥 D、正方体3. 我市2014年参加中考的考生人数约为43400人,将43400用科学记数法表示为( )A、434×102 B、43.4×103 C、4.34×104 D、0.434×1054. 体育课上,两名同学分别进行了5次立定跳远测试,要判断这5次测试中谁的成绩比较稳定,通常需要比较这两名同学成绩的( )A、平均数 B、中位数 C、众数 D、方差5. 下列运算正确的是( )A、 = + B、( )2=3 C、3a﹣a=3 D、(a2)3=a56. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、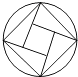 C、
C、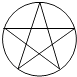 D、
D、 7. 若x1 , x2是一元二次方程x2+10x+16=0的两个根,则x1+x2的值是( )A、﹣10 B、10 C、﹣16 D、168. 不等式组 的整数解共有( )A、1个 B、2个 C、3个 D、4个9. 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2 , 连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )
7. 若x1 , x2是一元二次方程x2+10x+16=0的两个根,则x1+x2的值是( )A、﹣10 B、10 C、﹣16 D、168. 不等式组 的整数解共有( )A、1个 B、2个 C、3个 D、4个9. 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2 , 连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )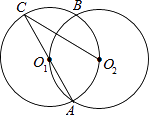 A、60° B、45° C、30° D、20°10. 如图,等腰梯形ABCD的对角线长为13,点E、F、G、H分别是边AB、BC、CD、DA的中点,则四边形EFGH的周长是( )
A、60° B、45° C、30° D、20°10. 如图,等腰梯形ABCD的对角线长为13,点E、F、G、H分别是边AB、BC、CD、DA的中点,则四边形EFGH的周长是( )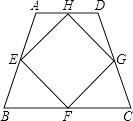 A、13 B、26 C、36 D、3911. 如图,正比例函数y=x与反比例函数y= 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于y= 的函数值时,x的取值范围是( )
A、13 B、26 C、36 D、3911. 如图,正比例函数y=x与反比例函数y= 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于y= 的函数值时,x的取值范围是( )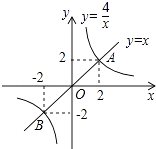 A、x>2 B、x<﹣2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>212. 如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离的走法共有( )
A、x>2 B、x<﹣2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>212. 如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离的走法共有( )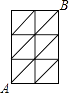 A、1种 B、2种 C、3种 D、4种
A、1种 B、2种 C、3种 D、4种二、填空题
-
13. |﹣8|= .14. 如图,直线a、b相交于点O,∠1=50°,则∠2=度.
 15. 分解因式:a2b﹣b3= .16. 如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为 .
15. 分解因式:a2b﹣b3= .16. 如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为 .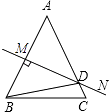 17.
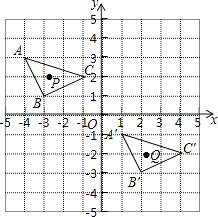
17.如图,△A′B′C′是△ABC经过某种变换后得到的图形,如果△ABC中有一点P的坐标为(a,2),那么变换后它的对应点Q的坐标为 .
 18. 甲、乙、丙三位同学进行报数游戏,游戏规则为:甲报1,乙报2,丙报3,再甲报4,乙报5,丙报6,…依次循环反复下去,当报出的数为2014时游戏结束,若报出的数是偶数,则该同学得1分.当报数结束时甲同学的得分是分.
18. 甲、乙、丙三位同学进行报数游戏,游戏规则为:甲报1,乙报2,丙报3,再甲报4,乙报5,丙报6,…依次循环反复下去,当报出的数为2014时游戏结束,若报出的数是偶数,则该同学得1分.当报数结束时甲同学的得分是分.三、解答题
-
19. 计算:(﹣2)2+(﹣3)×2﹣ .20. 如图,在正方形ABCD中,E、F分别是AB、BC上的点,且AE=BF.求证:CE=DF.
 21. 某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图.
21. 某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图.
请根据图中提供的信息解答下列问题:
(1)、在这次调查中共调查了名学生;扇形统计图中方案1所对应的圆心角的度数为度;(2)、请把条形统计图补充完整;(3)、已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人?22. 甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.23. 某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题: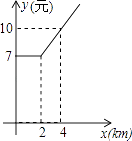 (1)、该地出租车的起步价是元;(2)、当x>2时,求y与x之间的函数关系式;(3)、若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?24.
(1)、该地出租车的起步价是元;(2)、当x>2时,求y与x之间的函数关系式;(3)、若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?24.如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: ≈1.41, ≈1.73).
 25. 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
25. 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.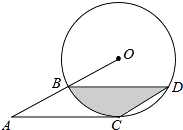 (1)、求证:AC是⊙O的切线;(2)、求弦BD的长;(3)、求图中阴影部分的面积.26.
(1)、求证:AC是⊙O的切线;(2)、求弦BD的长;(3)、求图中阴影部分的面积.26.如图,在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
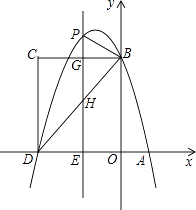 (1)、求该抛物线的解析式;(2)、当点P在直线BC上方时,请用含m的代数式表示PG的长度;(3)、在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、当点P在直线BC上方时,请用含m的代数式表示PG的长度;(3)、在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.