2019年高考数学二轮复习专题10:解析几何
试卷更新日期:2019-03-13 类型:二轮复习
一、单选题
-
1. 已知双曲线 的一个焦点与圆 的圆心重合,且双曲线的离心率等于 ,则该双曲线的标准方程为( )A、
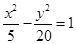 B、
B、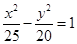 C、
C、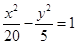 D、
D、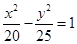 2. 已知抛物线 的准线过双曲线 的左焦点且与双曲线交于 、 两点, 为坐标原点,且 的面积为 ,则双曲线的离心率为A、 B、4 C、3 D、23. 圆 与圆 的公切线条数为( )A、1 B、2 C、3 D、44. 已知椭圆的两个焦点是 ,且点 在椭圆上,则椭圆的标准方程是( )A、
2. 已知抛物线 的准线过双曲线 的左焦点且与双曲线交于 、 两点, 为坐标原点,且 的面积为 ,则双曲线的离心率为A、 B、4 C、3 D、23. 圆 与圆 的公切线条数为( )A、1 B、2 C、3 D、44. 已知椭圆的两个焦点是 ,且点 在椭圆上,则椭圆的标准方程是( )A、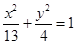 B、
B、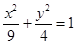 C、
C、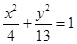 D、
D、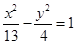 5. 椭圆 的左焦点为 ,直线 与椭圆相交于点 ,当 的周长最大时, 的面积是( )A、
5. 椭圆 的左焦点为 ,直线 与椭圆相交于点 ,当 的周长最大时, 的面积是( )A、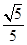 B、
B、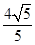 C、
C、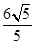 D、
D、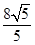 6. 圆 的圆心到直线 的距离为1,则 ( )A、
6. 圆 的圆心到直线 的距离为1,则 ( )A、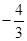 B、
B、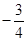 C、
C、 D、2
7. 如图,双曲线 的左、右焦点分别是 , , 是双曲线右支上一点, 与圆 相切于点 , 是 的中点,则 ( )
D、2
7. 如图,双曲线 的左、右焦点分别是 , , 是双曲线右支上一点, 与圆 相切于点 , 是 的中点,则 ( )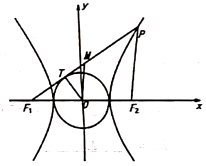 A、1 B、2 C、 D、
A、1 B、2 C、 D、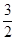 8. 已知椭圆 的两个焦点为F1 , F2 , 弦AB过点F1 , 则△ABF2的周长为( ).A、10 B、20 C、
8. 已知椭圆 的两个焦点为F1 , F2 , 弦AB过点F1 , 则△ABF2的周长为( ).A、10 B、20 C、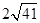 D、
D、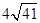 9. 已知椭圆 上任一点到两焦点的距离分别为 , ,焦距为 ,若 , , 成等差数列,则椭圆的离心率为( )A、 B、
9. 已知椭圆 上任一点到两焦点的距离分别为 , ,焦距为 ,若 , , 成等差数列,则椭圆的离心率为( )A、 B、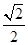 C、
D、
10. 曲线y= x2-2x在点 处的切线的倾斜角为( ).A、-135° B、45° C、-45° D、135°11. 阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数 且 )的点的轨迹是圆,后人将这个圆称为阿氏圆.若平面内两定点 间的距离为2,动点 满足 当 不共线时, 面积的最大值是( )A、 B、 C、
C、
D、
10. 曲线y= x2-2x在点 处的切线的倾斜角为( ).A、-135° B、45° C、-45° D、135°11. 阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数 且 )的点的轨迹是圆,后人将这个圆称为阿氏圆.若平面内两定点 间的距离为2,动点 满足 当 不共线时, 面积的最大值是( )A、 B、 C、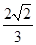 D、
D、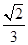 12. 已知椭圆 ,与双曲线 具有相同焦点F1、F2 , 且在第一象限交于点P,椭圆与双曲线的离心率分别为e1、e2 , 若∠F1PF2= ,则 的最小值是( )A、
12. 已知椭圆 ,与双曲线 具有相同焦点F1、F2 , 且在第一象限交于点P,椭圆与双曲线的离心率分别为e1、e2 , 若∠F1PF2= ,则 的最小值是( )A、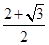 B、2+
C、
B、2+
C、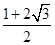 D、
D、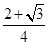
二、填空题
-
13. 两直线 与 平行,则它们之间的距离为.14. 已知抛物线 的焦点为 .若抛物线上存在点 ,使得线段 的中点的横坐标为 ,则 .15. 已知直线l:mx﹣y=1,若直线l与直线x+m(m﹣1)y=2垂直,则m的值为 , 动直线l:mx﹣y=1被圆C:x2﹣2x+y2﹣8=0截得的最短弦长为 .16. 过动点 作圆: 的切线 ,其中 为切点,若 ( 为坐标原点),则 的最小值是.17. AB为过抛物线 焦点F的一条弦,设 , ,以下结论正确的是 ,
,且 的最小值为4 以AF为直径的圆与x轴相切.
18. 如图,已知 , 分别是椭圆 的左,右焦点, , , 是椭圆上 轴上方的三点,且 ( 为坐标原点),则 的取值范围是 .
三、解答题
-
19. 已知圆C与y轴相切,圆心C在直线 上,且截直线 的弦长为 ,求圆C的方程.20. 已知曲线C的极坐标方程为 以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程为 为参数 .(1)、判断直线l与曲线C的位置关系,并说明理由;(2)、若直线l和曲线C相交于A,B两点,求 .21. 抛物线 的焦点为 ,过点 的直线交抛物线于 , 两点.(1)、 为坐标原点,求证: ;(2)、设点 在线段 上运动,原点 关于点 的对称点为 ,求四边形 面积的最小值22. 已知椭圆 上的点 (不包括横轴上点)满足:与 , 两点连线的斜率之积等于 , , 两点也在曲线 上.(1)、求椭圆 的方程;(2)、过椭圆 的右焦点作斜率为1的直线交椭圆于 , 两点,求 ;(3)、求椭圆上的点到直线 距离的最小值.23. 已知抛物线 过点 .
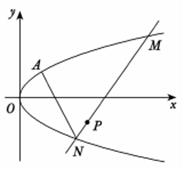 (1)、求抛物线C的方程;(2)、求过点 的直线与抛物线C交于M,N两个不同的点(均与点A不重合).设直线AM,AN的斜率分别为 , ,求证: 为定值.24. 已知椭圆 的焦距为8,其短轴的两个端点与长轴的个端点构成正三角形.(1)、求 的方程;(2)、设 为 的左焦点, 为直线 上任意一点,过点 作 的垂线交 于两点 .
(1)、求抛物线C的方程;(2)、求过点 的直线与抛物线C交于M,N两个不同的点(均与点A不重合).设直线AM,AN的斜率分别为 , ,求证: 为定值.24. 已知椭圆 的焦距为8,其短轴的两个端点与长轴的个端点构成正三角形.(1)、求 的方程;(2)、设 为 的左焦点, 为直线 上任意一点,过点 作 的垂线交 于两点 .(ⅰ)证明: 平分线段 (其中 为坐标原点);
(ⅱ)当 取最小值时,求点 的坐标.