2019年高考数学二轮复习专题09:立体几何
试卷更新日期:2019-03-13 类型:二轮复习
一、单选题
-
1. 《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA₁是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点,以AA₁为底面矩形的一边,则这样的阳马的个数是( )
 A、4 B、8 C、12 D、162. 一个几何体的三视图如图所示,则该几何体的表面积为( )
A、4 B、8 C、12 D、162. 一个几何体的三视图如图所示,则该几何体的表面积为( ) A、3π B、4π C、2π+4 D、3π+43. 已知直线 平面 ,直线 平面 ,则下列四个命题正确的是( )
A、3π B、4π C、2π+4 D、3π+43. 已知直线 平面 ,直线 平面 ,则下列四个命题正确的是( ); ; ; .
A、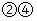 B、
B、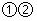 C、
C、 D、
D、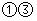 4. 某几何体的三视图如图所示(单位: ),则该几何体的体积(单位: )是( )
4. 某几何体的三视图如图所示(单位: ),则该几何体的体积(单位: )是( ) A、
A、 B、54
C、
B、54
C、 D、108
5. 已知图中的网格是由边长为1的小正方形组成的,一个几何体的三视图如图中的粗实线和粗虚线所示,则这个几何体的体积为( )
D、108
5. 已知图中的网格是由边长为1的小正方形组成的,一个几何体的三视图如图中的粗实线和粗虚线所示,则这个几何体的体积为( ) A、64 B、
A、64 B、 C、
C、 D、128
6. 如图,正三棱柱 中, , 是 的中点,则 与平面 所成角的正弦值等于( )
D、128
6. 如图,正三棱柱 中, , 是 的中点,则 与平面 所成角的正弦值等于( ) A、
A、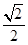 B、
C、
B、
C、 D、
D、 7. 如图,四棱柱 的底面是菱形且 平面ABCD,则 与BD所成的角是
7. 如图,四棱柱 的底面是菱形且 平面ABCD,则 与BD所成的角是 A、
A、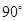 B、
B、 C、
C、 D、
D、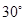 8. 在四面体ABCD中,已知棱AC的长为 ,其余各棱长都为1,则二面角A-CD-B的余弦值为 ( )A、 B、 C、 D、
8. 在四面体ABCD中,已知棱AC的长为 ,其余各棱长都为1,则二面角A-CD-B的余弦值为 ( )A、 B、 C、 D、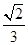 9. 如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A、
9. 如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A、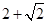 B、
B、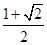 C、
C、 D、
D、
二、填空题
-
10. 如图,半球内有一内接正四棱锥 ,该四棱锥的体积为 ,则该半球的体为.

三、解答题
-
11. 已知三棱柱ABC﹣A′B′C′的底面为直角三角形,两条直角边AC和BC的长分别为4和3,侧棱AA′的长为10.
(1)若侧棱AA′垂直于底面,求该三棱柱的表面积;
(2)若侧棱AA′与底面所成的角为60°,求该三棱柱的体积.
12. 如图,在直三棱柱 侧棱和底面垂直的棱柱 中,平面 侧面 , ,线段AC、 上分别有一点E、F且满足 , .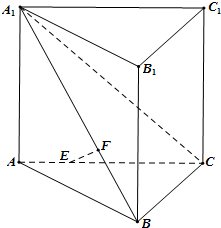 (1)、求证: ;(2)、求点E到直线 的距离;(3)、求二面角 的平面角的余弦值.13. 在三棱台 中, 是等边三角形,二面角 的平面角为 , .
(1)、求证: ;(2)、求点E到直线 的距离;(3)、求二面角 的平面角的余弦值.13. 在三棱台 中, 是等边三角形,二面角 的平面角为 , .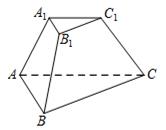
(I)求证: ;
(II)求直线 与平面 所成角的正弦值.
14. 已知 两两垂直, , 为 的中点,点 在 上, .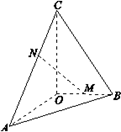
(Ⅰ)求 的长;
(Ⅱ)若点 在线段 上,设 ,当 时,求实数 的值.
15. 如图,四棱锥 中,底面四边形 为菱形, , 为等边三角形.
(Ⅰ)求证: ;
(Ⅱ)若 ,求直线 与平面 所成的角.
16. 在四面体ABCD中,过棱AB的上一点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H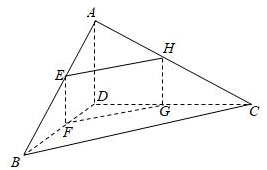 (1)、求证:截面EFGH为平行四边形(2)、若P、Q在线段BD、AC上, ,且P、F不重合,证明:PQ∥截面EFGH17. 如图,边长为 的等边三角形 所在的平面垂直于矩形 所在的平面, , 为 的中点.
(1)、求证:截面EFGH为平行四边形(2)、若P、Q在线段BD、AC上, ,且P、F不重合,证明:PQ∥截面EFGH17. 如图,边长为 的等边三角形 所在的平面垂直于矩形 所在的平面, , 为 的中点. (1)、证明: ;(2)、求点 到平面 的距离.18. 如图,在三棱锥 中, , , °,平面 平面 , 分别为 中点.
(1)、证明: ;(2)、求点 到平面 的距离.18. 如图,在三棱锥 中, , , °,平面 平面 , 分别为 中点. (1)、求证: 平面 ;(2)、求二面 的大小.19. 如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD.
(1)、求证: 平面 ;(2)、求二面 的大小.19. 如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD. (1)、求证:BD⊥平面ECD;(2)、求D点到面CEB的距离.20. 如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
(1)、求证:BD⊥平面ECD;(2)、求D点到面CEB的距离.20. 如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.(Ⅰ)设点M为棱PD中点,求证:EM∥平面ABCD;
(Ⅱ)线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于 ?若存在,试确定点N的位置;若不存在,请说明理由.
 21. 如图,在矩形ABCD中, ,点M在边DC上,点F在边AB上,且 ,垂足为E,若将 沿AM折起,使点D位于 位置,连接 , 得四棱锥 .
21. 如图,在矩形ABCD中, ,点M在边DC上,点F在边AB上,且 ,垂足为E,若将 沿AM折起,使点D位于 位置,连接 , 得四棱锥 .
Ⅰ 求证: ;
Ⅱ 若 ,直线
 与平面ABCM所成角的大小为 ,求直线 与平面ABCM所成角的正弦值.22. 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.
与平面ABCM所成角的大小为 ,求直线 与平面ABCM所成角的正弦值.22. 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.(Ⅰ)求证:AD⊥平面BFED;
(Ⅱ)在线段EF上是否存在一点P,使得平面PAB与平面ADE所成的锐二面角的余弦值为 .若存在,求出点P的位置;若不存在,说明理由.
 23. 如图,在四棱锥 中,底面 是直角梯形,侧棱 底面 , 垂直于 和 , 为棱 上的点, , .
23. 如图,在四棱锥 中,底面 是直角梯形,侧棱 底面 , 垂直于 和 , 为棱 上的点, , . (1)、若 为棱 的中点,求证: 平面 ;(2)、当 时,求平面 与平面 所成的锐二面角的余弦值;(3)、在第(2)问条件下,设点 是线段 上的动点, 与平面 所成的角为 ,求当 取最大值时点 的位置.
(1)、若 为棱 的中点,求证: 平面 ;(2)、当 时,求平面 与平面 所成的锐二面角的余弦值;(3)、在第(2)问条件下,设点 是线段 上的动点, 与平面 所成的角为 ,求当 取最大值时点 的位置.
-