2014年广西柳州市中考数学试卷

试卷更新日期：2017-04-25 类型：中考真卷

进入出卷网下载

一、选择题

1. 如图，李师傅做了一个零件，请你告诉他这个零件的主视图是（）

A、 B、 C、 D、

查看试题解析
2. 在所给的 $\frac{1}{3}$ ，0，﹣1，3这四个数中，最小的数是（）

A、 $\frac{1}{3}$ B、0 C、﹣1 D、3

查看试题解析
3. 下列选项中，属于无理数的是（）

A、2 B、π C、 $\frac{3}{2}$ D、﹣2

查看试题解析
4. 如图，直线l∥OB，则∠1的度数是（）

A、120° B、30° C、40° D、60°

查看试题解析
5. 下列计算正确的选项是（）

A、 $\sqrt{4}$ ﹣1= $\sqrt{3}$ B、（ $\sqrt{5}$ ）²=5 C、2a﹣b=ab D、 $\frac{2}{y} + \frac{1}{y}$ = $\frac{3}{2 y}$

查看试题解析
6. 如图，直角坐标系中的五角星关于y轴对称的图形在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 学校“清洁校园”环境爱护志愿者的年龄分布如图，那么这些志愿者年龄的众数是（）

A、12岁 B、13岁 C、14岁 D、15岁

查看试题解析
8. 如图，当半径分别是5和r的两圆⊙O₁和⊙O₂外切时，它们的圆心距O₁O₂=8，则⊙O₂的半径r为（）

A、12 B、8 C、5 D、3

查看试题解析
9. 在下列所给出的4个图形中，对角线一定互相垂直的是（）

A、长方形 B、平行四边形 C、菱形 D、直角梯形

查看试题解析
10. 如图，正六边形的每一个内角都相等，则其中一个内角α的度数是（）

A、240° B、120° C、60° D、30°

查看试题解析
11. 小兰画了一个函数y=x²+ax+b的图象如图，则关于x的方程x²+ax+b=0的解是（）

A、无解 B、x=1 C、x=﹣4 D、x=﹣1或x=4

查看试题解析
12. 如图，每个灯泡能否通电发光的概率都是0.5，当合上开关时，至少有一个灯泡发光的概率是（）

A、0.25 B、0.5 C、0.75 D、0.95

查看试题解析

二、填空题

13. 3的相反数为．

查看试题解析
14.
如图，身高为x cm的1号同学与身高为y cm的2号同学站在一起时，如果用一个不等式来表示他们的身高关系，则这个式子可以表示成xy（用“＞”或“＜”填空）．

查看试题解析
15. 如图，等腰梯形ABCD的周长为16，BC=4，CD=3，则AB= ．

查看试题解析
16. 方程 $\frac{2}{x}$ ﹣1=0的解是x= ．

查看试题解析
17. 将直线y= $\frac{1}{2}$ x向上平移个单位后得到直线y= $\frac{1}{2}$ x+7．

查看试题解析
18.
如图，在△ABC中，分别以AC，BC为边作等边△ACD和等边△BCE．设△ACD、△BCE、△ABC的面积分别是S₁、S₂、S₃ ，现有如下结论：

①S₁：S₂=AC²：BC²；
②连接AE，BD，则△BCD≌△ECA；
③若AC⊥BC，则S₁•S₂= $\frac{3}{4}$ S₃² ．
其中结论正确的序号是．

查看试题解析

三、解答题

19. 计算：2×（﹣5）+3．

查看试题解析
20. 一位射击运动员在10次射击训练中，命中靶的环数如图．
请你根据图表，完成下列问题：

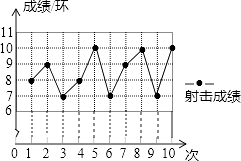(1)、补充完成下面成绩表单的填写：
射击序次
1
2
3
4
5
6
7
8
9
10
成绩/环
8
10
7
9
10
7
10

(2)、求该运动员这10次射击训练的平均成绩．

查看试题解析
21. 小张把两个大小不同的苹果放到天平上称，当天平保持平衡时的砝码重量如图所示．问：这两个苹果的重量分别为多少g？

查看试题解析
22.
如图，在△ABC中，BD⊥AC，AB=6，AC=5 $\sqrt{3}$ ，∠A=30°．

①求BD和AD的长；
②求tanC的值．

查看试题解析
23. 如图，函数y= $\frac{k}{x}$ 的图象过点A（1，2）．

(1)、求该函数的解析式；

(2)、过点A分别向x轴和y轴作垂线，垂足为B和C，求四边形ABOC的面积；

(3)、求证：过此函数图象上任意一点分别向x轴和y轴作垂线，这两条垂线与两坐标轴所围成矩形的面积为定值．

查看试题解析
24. 如图，在△ABC中，∠BAC的角平分线AD交BC于E，交△ABC的外接圆⊙O于D．

(1)、求证：△ABE∽△ADC；

(2)、请连接BD，OB，OC，OD，且OD交BC于点F，若点F恰好是OD的中点．求证：四边形OBDC是菱形．

查看试题解析
25. 如图，正方形ABCD的边长为1，AB边上有一动点P，连接PD，线段PD绕点P顺时针旋转90°后，得到线段PE，且PE交BC于F，连接DF，过点E作EQ⊥AB的延长线于点Q．

(1)、求线段PQ的长；

(2)、问：点P在何处时，△PFD∽△BFP，并说明理由．

查看试题解析
26. 已知二次函数图象的顶点坐标为（0，1），且过点（﹣1， $\frac{5}{4}$ ），直线y=kx+2与y轴相交于点P，与二次函数图象交于不同的两点A（x₁ ， y₁），B（x₂ ， y₂）．
（注：在解题过程中，你也可以阅读后面的材料）
附：阅读材料
   任何一个一元二次方程的根与系数的关系为：两根的和等于一次项系数与二次项系数的比的相反数，两根的积等于常数项与二次项系数的比．
   即：设一元二次方程ax²+bx+c=0的两根为x₁ ， x₂ ，
   则：x₁+x₂=﹣ $\frac{b}{a}$ ，x₁•x₂= $\frac{c}{a}$
   能灵活运用这种关系，有时可以使解题更为简单．
   例：不解方程，求方程x²﹣3x=15两根的和与积．
   解：原方程变为：x²﹣3x﹣15=0
∵一元二次方程的根与系数有关系：x₁+x₂=﹣ $\frac{b}{a}$ ，x₁•x₂= $\frac{c}{a}$
∴原方程两根之和=﹣ $\frac{- 3}{1}$ =3，两根之积= $\frac{- 15}{1}$ =﹣15．

(1)、求该二次函数的解析式．

(2)、对（1）中的二次函数，当自变量x取值范围在﹣1＜x＜3时，请写出其函数值y的取值范围；（不必说明理由）

(3)、求证：在此二次函数图象下方的y轴上，必存在定点G，使△ABG的内切圆的圆心落在y轴上，并求△GAB面积的最小值．

查看试题解析

射击序次	1	2	3	4	5	6	7	8	9	10
成绩/环				8	10	7	9	10	7	10