2018-2019学年初中数学北师大版八年级下册4.3公式法 同步练习
试卷更新日期:2019-03-13 类型:同步测试
一、单选题
-
1. 下列因式分解结果正确的是( ).A、
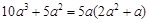 B、
B、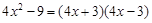 C、
C、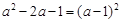 D、
D、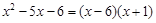 2. 因式分解x﹣4x3的最后结果是( )A、x(1﹣2x)2 B、x(2x﹣1)(2x+1) C、x(1﹣2x)(2x+1) D、x(1﹣4x2)3. 若x﹣y+3=0,则x(x﹣4y)+y(2x+y)的值为( )A、9 B、﹣9 C、3 D、﹣34. 从边长为a的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )
2. 因式分解x﹣4x3的最后结果是( )A、x(1﹣2x)2 B、x(2x﹣1)(2x+1) C、x(1﹣2x)(2x+1) D、x(1﹣4x2)3. 若x﹣y+3=0,则x(x﹣4y)+y(2x+y)的值为( )A、9 B、﹣9 C、3 D、﹣34. 从边长为a的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )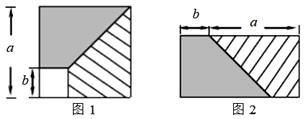 A、(a-b)2=a2-2ab+b2 B、a2-b2=(a+b)(a-b) C、(a+b)2=a2+2ab+b2 D、a2+ab=a(a+b)5. 小明在抄分解因式的题目时,不小心漏抄了x的指数,他只知道该数为不大于10的正整数,并且能利用平方差公式分解因式,他抄在作业本上的式子是x□﹣4y2(“□”表示漏抄的指数),则这个指数可能的结果共有( )
A、(a-b)2=a2-2ab+b2 B、a2-b2=(a+b)(a-b) C、(a+b)2=a2+2ab+b2 D、a2+ab=a(a+b)5. 小明在抄分解因式的题目时,不小心漏抄了x的指数,他只知道该数为不大于10的正整数,并且能利用平方差公式分解因式,他抄在作业本上的式子是x□﹣4y2(“□”表示漏抄的指数),则这个指数可能的结果共有( )
A、2种 B、3种 C、4种 D、5种6. 将9.52变形正确的是( )
A、9.52=92+0.52 B、9.52=(10+0.5)(10﹣0.5) C、9.52=102﹣2×10×0.5+0.52 D、9.52=92+9×0.5+0.527. 对于非零的两个实数a,b,规定 ,那么将 结果再进行分解因式,则为( )A、a(a+2)(a-2) B、a(a+4)(a-4) C、(a+4)(a-4) D、a(a2+4)8. 下列多项式中,在有理数范围内能够分解因式的是( )A、 ﹣5 B、 +5x+3 C、 0.25 ﹣16 D、 +9
D、 +9  9. 若n为任意正整数,(n+11)2-n2的值总可以被k整除,则k等于( )
9. 若n为任意正整数,(n+11)2-n2的值总可以被k整除,则k等于( )
A、11 B、22 C、11或22 D、11的倍数10. 一次课堂练习,小颖同学做了以下几道因式分解题,你认为她做得不够完整的是( )A、x3-x=x(x2-1) B、x2y-y3=y(x+y)(x-y) C、-m2+4n2=(2n+m)(2n-m) D、3p2-27q2=3(p+3q)(p-3q)二、填空题
-
11. 分解因式: = .12. 已知 ,那么 的值为 .13. 把多项式3x2﹣12因式分解的结果是 .14. 在日常生活中,如取款、上网需要密码,有一种因式分解法产生密码,例如x4-y4=(x-y)(x+y)(x2+y2),当x=9,y=9时,x-y=0,x+y=18,x2+y2=162,则密码018162. 对于多项式4x3-xy2 , 取x=10,y=10,用上述方法产生密码是(写出一个即可).15. 设a,b是直角三角形的两条直角边的长,且 ,则直角三角形的斜边长为 .
16. 分解因式: .三、解答题
-
17. 如图,在一个大圆盘中,镶嵌着四个大小一样的小圆盘,已知大小圆盘的半径都是整数,阴影部分的面积为5πcm2 , 请你求出大小两个圆盘的半径.
 18. 把下列多项式分解因式(1)、2x2y-6xy;(2)、x2+4x+4;(3)、16a2-4b2.19. 因式分解:(1)、20a3﹣30a2(2)、16﹣(2a+3b)2(3)、﹣16x2y2+12xy3z(4)、5x2y﹣25x2y2+40x3y20. 已知(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2 .
18. 把下列多项式分解因式(1)、2x2y-6xy;(2)、x2+4x+4;(3)、16a2-4b2.19. 因式分解:(1)、20a3﹣30a2(2)、16﹣(2a+3b)2(3)、﹣16x2y2+12xy3z(4)、5x2y﹣25x2y2+40x3y20. 已知(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2 .求 的值.
21. 综合题
(1)、利用因式分解证明:257-512能被250整除.
(2)、233-2被11至20之间的两个数整除,求这两个数.
22. 已知三角形的三边长分别为 a,b,c,且满足等式 a2+b2+c2=ab+bc+ac,试猜想 该三角形的形状,并证明你的猜想.
23. 把一个边长a=84m的正方形广场的四角均留出一个边长b=8m的正方形修建花坛,其余地方种草,草坪的面积有多大如果种草坪每平方米需5元,那么给这个广场种草至少要投资多少钱元.24. 下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.解:设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步).
回答下列问题:
(1)、该同学第二步到第三步运用了因式分解的( )A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式(2)、该同学因式分解的结果(填“彻底”或“不彻底”),若不彻底,请直接写出因式分解的最后结果: .(3)、请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行分解.