2016-2017学年湖北省天门市七年级上学期期末数学试卷
试卷更新日期:2017-04-25 类型:期末考试
一、选择题:
-
1. 下列四个数中最小的数是( )A、3 B、0 C、﹣ D、42. 拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000kg,这个数据用科学记数法表示为( )A、0.5×1011kg B、50×109kg C、5×109kg D、5×1010kg3. 在下列式子 ,﹣3x,﹣ abc,a,0,a﹣b,0.95中,单项式有( )A、7个 B、6个 C、5个 D、4个4. 已知方程x2k﹣1+k=0是关于x的一元一次方程,则方程的解等于( )A、﹣1 B、1 C、 D、﹣5. 小丽制作了一个对面图案均相同的正方体礼品盒(如图所示),则这个正方体礼品盒的平面展开图可能是( )
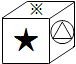 A、
A、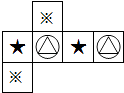 B、
B、 C、
C、 D、
D、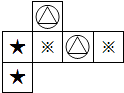 6. 已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是( )A、13x﹣1 B、6x2+13x﹣1 C、5x+1 D、﹣5x﹣17. 下列有理数大小关系判断正确的是( )A、0>|﹣10| B、﹣(﹣ )>﹣|﹣ | C、|﹣3|<|+3| D、﹣1>﹣0.018. 某种商品进价为a元,商店将价格提高30%作零售价销售.在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动.这时一件该商品的售价为( )A、a元 B、0.8a元 C、1.04a元 D、0.92a元9. 甲班有54人,乙班有48人,要使甲班人数是乙班的2倍,设从乙班调往甲班人数x,可列方程( )A、54+x=2(48﹣x) B、48+x=2(54﹣x) C、54﹣x=2×48 D、48+x=2×5410. 如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
6. 已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是( )A、13x﹣1 B、6x2+13x﹣1 C、5x+1 D、﹣5x﹣17. 下列有理数大小关系判断正确的是( )A、0>|﹣10| B、﹣(﹣ )>﹣|﹣ | C、|﹣3|<|+3| D、﹣1>﹣0.018. 某种商品进价为a元,商店将价格提高30%作零售价销售.在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动.这时一件该商品的售价为( )A、a元 B、0.8a元 C、1.04a元 D、0.92a元9. 甲班有54人,乙班有48人,要使甲班人数是乙班的2倍,设从乙班调往甲班人数x,可列方程( )A、54+x=2(48﹣x) B、48+x=2(54﹣x) C、54﹣x=2×48 D、48+x=2×5410. 如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )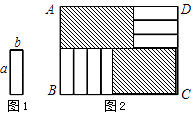 A、a=b B、a=3b C、a=2b D、a=4b
A、a=b B、a=3b C、a=2b D、a=4b二、填空题:
-
11. 如果x<0,y>0,且|x|=2,|y|=3,那么x+y= .12. 若5a2x﹣3b与﹣3a5b4y+5是同类项,则x= , y= .13.
如图,一个平衡的天平盘中,左盘有2个小正方体和2个小球,右盘有4个小正方体和1个小球.每个小球的重量用x克表示,小正方体每个5克,那么可列方程得 .
 14. 把一个周角7等分,每一份是度分(精确到1分).15. 如图,点O是直线l上一点,作射线OA,过O点作OB⊥OA于点O,则图中∠1,∠2的数量关系为 .
14. 把一个周角7等分,每一份是度分(精确到1分).15. 如图,点O是直线l上一点,作射线OA,过O点作OB⊥OA于点O,则图中∠1,∠2的数量关系为 .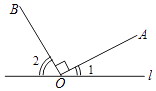 16. 小明在做作业时,不小心把方程中的一个常数污染了看不清楚,被污染的方程为: ■,怎么办?小明想了想,便翻看了书后的答案,此方程的解为 ,于是,他很快知道了这个常数,他补出的这个常数是 .
16. 小明在做作业时,不小心把方程中的一个常数污染了看不清楚,被污染的方程为: ■,怎么办?小明想了想,便翻看了书后的答案,此方程的解为 ,于是,他很快知道了这个常数,他补出的这个常数是 .三、解答题:
-
17. 计算:(1)、3xy﹣4xy﹣(﹣2xy)(2)、(﹣3)2÷2 ÷(﹣ )+4+22×(﹣ )18. 已知x= ,y=﹣2,求代数式3x2y﹣[2xy2﹣2(2xy﹣ x2y)+xy]+2xy2的值.19. 解下列方程:(1)、5(x+8)﹣5=﹣6(2x﹣7)(2)、 = +2.20. 问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长.
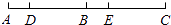
请补全以下解答过程.
解:∵D,B,E三点依次在线段AC上,
∴DE=+BE.
∵AD=BE,
∴DE=DB+=AB.
∵DE=4,
∴AB=4.
∵ ,
∴AC=2AB= .
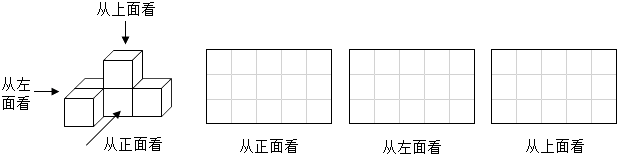
21.从正面、左面、上面观察如图所示的几何体,分别画出你所看到的平面图形.
 22. 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
22. 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数. 23. 如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB、CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点随之停止运动.(设运动时间为t秒)
23. 如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB、CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点随之停止运动.(设运动时间为t秒)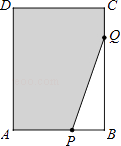 (1)、如果存在某一时刻恰好使QB=2PB,求出此时t的值;(2)、在(1)的条件下,求图中阴影部分的面积(结果保留整数).24. 陈老师打算购买装扮学校“六一”儿童节活动会场,气球种类有笑脸和爱心两种.两种气球的价格不同,但同一种类的气球价格相同.由于会场布置需要,购买了的三束气球(每束4个气球),每束价格如图所示.
(1)、如果存在某一时刻恰好使QB=2PB,求出此时t的值;(2)、在(1)的条件下,求图中阴影部分的面积(结果保留整数).24. 陈老师打算购买装扮学校“六一”儿童节活动会场,气球种类有笑脸和爱心两种.两种气球的价格不同,但同一种类的气球价格相同.由于会场布置需要,购买了的三束气球(每束4个气球),每束价格如图所示. (1)、若笑脸气球的单价是x元,请用含x的代数式表示第②束、第③束气球的总价格;(要求化简后,填在图形中)(2)、若第②束气球的总价钱比第③束气球的总价钱少2元,求这两种类的气球的单价.25. 如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将有一30度角的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°)
(1)、若笑脸气球的单价是x元,请用含x的代数式表示第②束、第③束气球的总价格;(要求化简后,填在图形中)(2)、若第②束气球的总价钱比第③束气球的总价钱少2元,求这两种类的气球的单价.25. 如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将有一30度角的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°)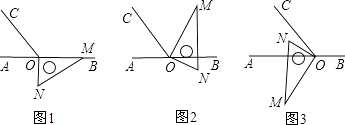 (1)、将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;(2)、将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;(3)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
(1)、将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;(2)、将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;(3)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.