2018-2019学年初中数学北师大版八年级下册3.2图形的旋转 同步练习
试卷更新日期:2019-03-13 类型:同步测试
一、单选题
-
1. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC',若∠B=78°,则∠CC'B'的大小是( )
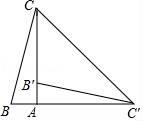 A、23° B、30° C、33° D、39°2. 如图,在Rt△ABC中,∠ACB=90° , ∠A=60° , AC=6,将△ABC绕点C按逆时针方向旋转得到△CDE , 此时点D恰好在AB边上,则点B与点E之间的距离为( )
A、23° B、30° C、33° D、39°2. 如图,在Rt△ABC中,∠ACB=90° , ∠A=60° , AC=6,将△ABC绕点C按逆时针方向旋转得到△CDE , 此时点D恰好在AB边上,则点B与点E之间的距离为( )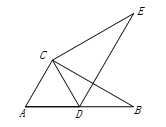 A、 B、 C、
A、 B、 C、 D、
3. 如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是( )
D、
3. 如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是( ) A、30° B、60° C、72° D、90°4. 如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )
A、30° B、60° C、72° D、90°4. 如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )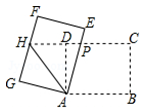 A、24 B、20 C、18 D、155. 若干个正方形按如图方式拼接,三角形M经过旋转变换能得到三角形N,下列四个点能作为旋转中心的是( )
A、24 B、20 C、18 D、155. 若干个正方形按如图方式拼接,三角形M经过旋转变换能得到三角形N,下列四个点能作为旋转中心的是( ) A、点A B、点B C、点C D、点D6. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC',若∠B =78°,则∠CC'B'的大小是( )
A、点A B、点B C、点C D、点D6. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC',若∠B =78°,则∠CC'B'的大小是( )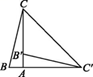 A、23° B、30° C、33° D、39°7. △ABC是等边三角形,点P在△ABC内,PA=2,将△PAB绕点A逆时针旋转得到△P1AC,则P1P的长等于( )
A、23° B、30° C、33° D、39°7. △ABC是等边三角形,点P在△ABC内,PA=2,将△PAB绕点A逆时针旋转得到△P1AC,则P1P的长等于( )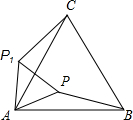 A、2 B、 C、 D、18. 如图,将边长为 的正方形绕点 逆时针旋转 ,那么图中阴影部分的面积为( )
A、2 B、 C、 D、18. 如图,将边长为 的正方形绕点 逆时针旋转 ,那么图中阴影部分的面积为( )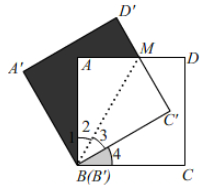 A、
A、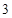 B、
C、
B、
C、 D、
D、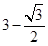 9. 如图,矩形 的顶点 为坐标原点,点 在 轴上,点 的坐标为 .如果将矩形 绕点 旋转 旋转后的图形为矩形 ,那么点 的坐标为( )
9. 如图,矩形 的顶点 为坐标原点,点 在 轴上,点 的坐标为 .如果将矩形 绕点 旋转 旋转后的图形为矩形 ,那么点 的坐标为( )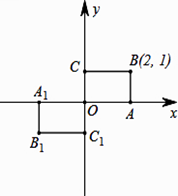 A、(2, 1) B、(-2, 1) C、(-2, -1) D、(2, -l)10. 如图甲,已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…如图乙,是六次旋转的位置图象,图中虚线是点M的运动轨迹,则在第四次旋转的过程中,点B,M间的距离可能是( )
A、(2, 1) B、(-2, 1) C、(-2, -1) D、(2, -l)10. 如图甲,已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…如图乙,是六次旋转的位置图象,图中虚线是点M的运动轨迹,则在第四次旋转的过程中,点B,M间的距离可能是( ) A、0.6 B、0.8 C、1.1 D、1.4
A、0.6 B、0.8 C、1.1 D、1.4二、填空题
-
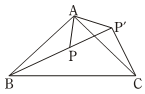
11. 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP绕点A逆时针旋转后与△ACP′重合,若AP=1,那么线段PP′的长等于 .
 12. 如图,在△ABC中,∠A=70°,AC=BC , 以点B为旋转中心把△ABC按顺时针方向旋转得到△A′BC′,点A′恰好落在边AC上,连接CC′,则∠ACC′= .
12. 如图,在△ABC中,∠A=70°,AC=BC , 以点B为旋转中心把△ABC按顺时针方向旋转得到△A′BC′,点A′恰好落在边AC上,连接CC′,则∠ACC′= .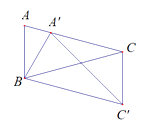 13. 在图中,是由基本图案多边形ABCDE旋转而成的,它的旋转角为 .
13. 在图中,是由基本图案多边形ABCDE旋转而成的,它的旋转角为 .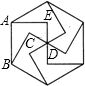 14. 如图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B' C′,则在旋转过程中点A、C′两点间的最大距离是.
14. 如图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B' C′,则在旋转过程中点A、C′两点间的最大距离是. 15. 如图Rt△ABC中,∠C=90°,∠B=50°,点D在边BC上,且BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度,若点B恰好落在初始Rt△ABC的边上,那么m=.
15. 如图Rt△ABC中,∠C=90°,∠B=50°,点D在边BC上,且BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度,若点B恰好落在初始Rt△ABC的边上,那么m=.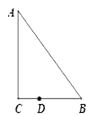 16. 如图,在 中, , ,以点 为旋转中心把 按顺时针旋转 度,得到 ,点 '恰好落在 上,连接CC′,则∠ACC'= .
16. 如图,在 中, , ,以点 为旋转中心把 按顺时针旋转 度,得到 ,点 '恰好落在 上,连接CC′,则∠ACC'= .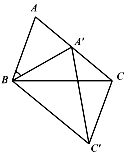 17. 定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.若△ABC经γ(1,180°)变换后得△A1B1C1 , △A1B1C1经γ(2,180°)变换后得△A2B2C2 , △A2B2C2经γ(3,180°)变换后得△A3B3C3 , 依此类推……△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn , 则点A1的坐标是 , 点A2020的坐标是 .
17. 定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.若△ABC经γ(1,180°)变换后得△A1B1C1 , △A1B1C1经γ(2,180°)变换后得△A2B2C2 , △A2B2C2经γ(3,180°)变换后得△A3B3C3 , 依此类推……△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn , 则点A1的坐标是 , 点A2020的坐标是 .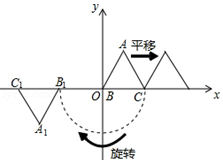
三、解答题
-
18. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
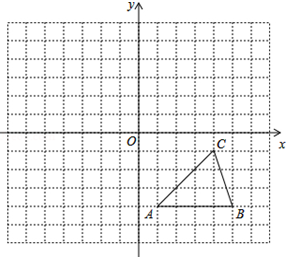
①已知△ABC与△A1B1C1关于原点O对称,请在图中画出△A1B1C1 , 并直接写出C点的对称点C1的坐标;
② 以原点O为旋转中心,将△ABC顺时针旋转90°得到△A2B2C2 , 请在图中画出△A2B2C2 , 并直接写出C点的对称点C2的坐标.19. 如图,△DEF是由△ABC通过一次旋转得到的,请用直尺和圆规画出旋转中心. 20. 如图,钟表的分针匀速旋转一周需要60分钟,那么:
20. 如图,钟表的分针匀速旋转一周需要60分钟,那么: (1)、它的旋转中心是什么?
(1)、它的旋转中心是什么?
(2)、分针旋转一周,时针旋转多少度?
(3)、上午8点整,时针和分针的夹角是多少?8点半呢?
21. 如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD.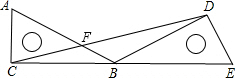 (1)、试判断△CBD的形状,并说明理由;(2)、求∠BDC的度数.22. 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点),
(1)、试判断△CBD的形状,并说明理由;(2)、求∠BDC的度数.22. 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点),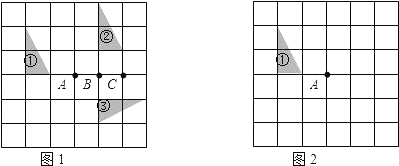 (1)、在图1中,图①经过一次变换(填“平移”或“旋转”或“轴对称”)可以得到图②;(2)、在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点(填“A”或 “B”或“C”);(3)、在图2中画出图①绕点A顺时针旋转90°后的图④.23. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
(1)、在图1中,图①经过一次变换(填“平移”或“旋转”或“轴对称”)可以得到图②;(2)、在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点(填“A”或 “B”或“C”);(3)、在图2中画出图①绕点A顺时针旋转90°后的图④.23. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.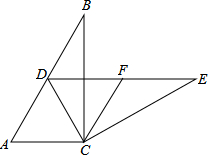 (1)、求n的值;(2)、若F是DE的中点,判断四边形ACFD的形状,并说明理由.
(1)、求n的值;(2)、若F是DE的中点,判断四边形ACFD的形状,并说明理由.