2014年广西贺州市中考数学试卷
试卷更新日期:2017-04-25 类型:中考真卷
一、选择题
-
1. 在﹣1、0、1、2这四个数中,最小的数是( )A、0 B、﹣1 C、1 D、22. 使分式 有意义,则x的取值范围是( )A、x≠1 B、x=1 C、x≤1 D、x≥13. 如图,OA⊥OB,若∠1=55°,则∠2的度数是( )
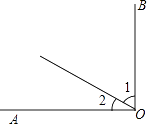 A、35° B、40° C、45° D、60°4. 未来三年,国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学记数法表示为( )A、0.845×104亿元 B、8.45×103亿元 C、8.45×104亿元 D、84.5×102亿元5. A、B、C、D四名选手参加50米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若A首先抽签,则A抽到1号跑道的概率是( )A、1 B、 C、 D、6. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、等腰梯形 B、平行四边形 C、正方形 D、正五边形7. 不等式 的解集在数轴上表示正确的是( )A、
A、35° B、40° C、45° D、60°4. 未来三年,国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学记数法表示为( )A、0.845×104亿元 B、8.45×103亿元 C、8.45×104亿元 D、84.5×102亿元5. A、B、C、D四名选手参加50米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若A首先抽签,则A抽到1号跑道的概率是( )A、1 B、 C、 D、6. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、等腰梯形 B、平行四边形 C、正方形 D、正五边形7. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、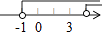 C、
C、 D、
D、 8. 如图是由5个大小相同的正方体组成的几何体,它的主视图是( )
8. 如图是由5个大小相同的正方体组成的几何体,它的主视图是( )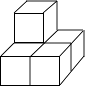 A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( )
9. 如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( )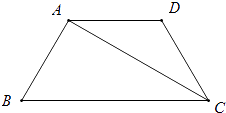 A、12 B、15 C、12 D、1510. 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数y= 在同一坐标系内的大致图象是( )
A、12 B、15 C、12 D、1510. 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数y= 在同一坐标系内的大致图象是( )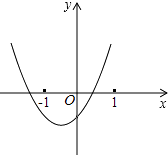 A、
A、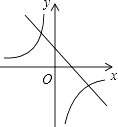 B、
B、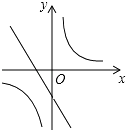 C、
C、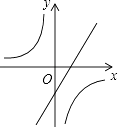 D、
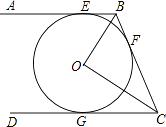
D、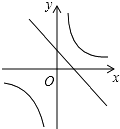 11. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE= ,CE=1.则 的长是( )
11. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE= ,CE=1.则 的长是( )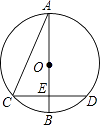 A、 B、 C、 D、12. 张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+ (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 ,矩形的周长是2(x+ );当矩形成为正方形时,就有x= (x>0),解得x=1,这时矩形的周长2(x+ )=4最小,因此x+ (x>0)的最小值是2.模仿张华的推导,你求得式子 (x>0)的最小值是( )A、2 B、1 C、6 D、10
A、 B、 C、 D、12. 张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+ (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 ,矩形的周长是2(x+ );当矩形成为正方形时,就有x= (x>0),解得x=1,这时矩形的周长2(x+ )=4最小,因此x+ (x>0)的最小值是2.模仿张华的推导,你求得式子 (x>0)的最小值是( )A、2 B、1 C、6 D、10二、填空题
-
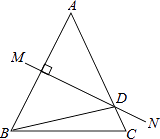
13. 因式分解:a3﹣4a= .14. 已知P1(1,y1),P2(2,y2)是正比例函数y= x的图象上的两点,则y1y2(填“>”或“<”或“=”).15. 近年来,A市民用汽车拥有量持续增长,2009年至2013年该市民用汽车拥有量(单位:万辆)依次为11,13,15,19,x.若这五个数的平均数为16,则x= .16. 已知关于x的方程x2+(1﹣m)x+ =0有两个不相等的实数根,则m的最大整数值是 .17. 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是 .
 18. 网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA= .
18. 网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA= .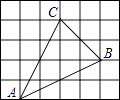
三、计算题
-
19. 计算下列各题(1)、计算:( ﹣2)0+(﹣1)2014+ ﹣sin45°;(2)、先化简,再求值:(a2b+ab)÷ ,其中a= +1,b= ﹣1.20. 已知关于x、y的方程组 的解为 ,求m、n的值.21. 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
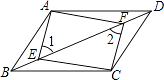 (1)、求证:BE=DF;(2)、求证:AF∥CE.22. 学习成为现代人的时尚,某市有关部门统计了最近6个月到图书馆的读者的职业分布情况,并做了下列两个不完整的统计图.
(1)、求证:BE=DF;(2)、求证:AF∥CE.22. 学习成为现代人的时尚,某市有关部门统计了最近6个月到图书馆的读者的职业分布情况,并做了下列两个不完整的统计图.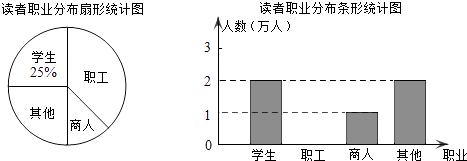 (1)、在统计的这段时间内,共有万人次到图书馆阅读,其中商人占百分比为 %;(2)、将条形统计图补充完整;(3)、若5月份到图书馆的读者共28000人次,估计其中约有多少人次读者是职工?23. 马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.24. 如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.
(1)、在统计的这段时间内,共有万人次到图书馆阅读,其中商人占百分比为 %;(2)、将条形统计图补充完整;(3)、若5月份到图书馆的读者共28000人次,估计其中约有多少人次读者是职工?23. 马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.24. 如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.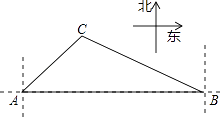 (1)、求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);(2)、求海轮在B处时与灯塔C的距离(结果保留整数).
(1)、求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);(2)、求海轮在B处时与灯塔C的距离(结果保留整数).(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)