2014年广西桂林市中考数学试卷
试卷更新日期:2017-04-25 类型:中考真卷
一、选择题
-
1. 2014的倒数是( )A、 B、﹣ C、|2014| D、﹣20142. 如图,已知AB∥CD,∠1=56°,则∠2的度数是( )
 A、34° B、56° C、65° D、124°3. 下列各式中,与2a的同类项的是( )A、3a B、2ab C、﹣3a2 D、a2b4. 在下列的四个几何体中,同一几何体的主视图与俯视图相同的是( )A、
A、34° B、56° C、65° D、124°3. 下列各式中,与2a的同类项的是( )A、3a B、2ab C、﹣3a2 D、a2b4. 在下列的四个几何体中,同一几何体的主视图与俯视图相同的是( )A、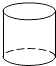 B、
B、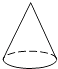 C、
C、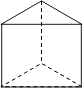 D、
D、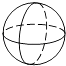 5. 在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点的坐标为( )A、(3,2) B、(2,﹣3) C、(﹣2,3) D、(﹣2,﹣3)6.
5. 在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点的坐标为( )A、(3,2) B、(2,﹣3) C、(﹣2,3) D、(﹣2,﹣3)6.一次函数y=kx+b(k≠0)的图象如图,则下列结论正确的是( )
 A、k=2 B、k=3 C、b=2 D、b=37. 下列命题中,是真命题的是( )A、等腰三角形都相似 B、等边三角形都相似 C、锐角三角形都相似 D、直角三角形都相似8. 两圆的半径分别为2和3,圆心距为7,则这两个圆的位置关系为( )A、外离 B、外切 C、相交 D、内切9. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
A、k=2 B、k=3 C、b=2 D、b=37. 下列命题中,是真命题的是( )A、等腰三角形都相似 B、等边三角形都相似 C、锐角三角形都相似 D、直角三角形都相似8. 两圆的半径分别为2和3,圆心距为7,则这两个圆的位置关系为( )A、外离 B、外切 C、相交 D、内切9. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 一个不透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球,则下列事件是必然事件的是( )A、摸出的四个球中至少有一个球是白球 B、摸出的四个球中至少有一个球是黑球 C、摸出的四个球中至少有两个球是黑球 D、摸出的四个球中至少有两个球是白球11. 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
10. 一个不透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球,则下列事件是必然事件的是( )A、摸出的四个球中至少有一个球是白球 B、摸出的四个球中至少有一个球是黑球 C、摸出的四个球中至少有两个球是黑球 D、摸出的四个球中至少有两个球是白球11. 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )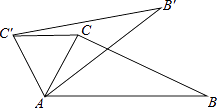 A、70° B、35° C、40° D、50°12.
A、70° B、35° C、40° D、50°12.如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1个单位长度分别沿B→A→D→C和B→C→D方向运动至相遇时停止.设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2,则下列结论错误的是( )
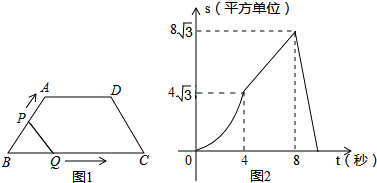 A、当t=4秒时,S=4 B、AD=4 C、当4≤t≤8时,S=2 t D、当t=9秒时,BP平分梯形ABCD的面积
A、当t=4秒时,S=4 B、AD=4 C、当4≤t≤8时,S=2 t D、当t=9秒时,BP平分梯形ABCD的面积二、填空题
-
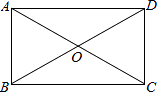
13. 分解因式:a2+2a= .14. 震惊世界的MH370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为 .15. 如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是 .
 16. 已知点P(1,﹣4)在反比例函数y= 的图象上,则k的值是 .17. 已知关于x的一元二次方程x2+(2k+1)x+k2﹣2=0的两根为x1和x2 , 且(x1﹣2)(x1﹣x2)=0,则k的值是 .18. 观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则81+82+83+84+…+82014的和的个位数字是 .
16. 已知点P(1,﹣4)在反比例函数y= 的图象上,则k的值是 .17. 已知关于x的一元二次方程x2+(2k+1)x+k2﹣2=0的两根为x1和x2 , 且(x1﹣2)(x1﹣x2)=0,则k的值是 .18. 观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则81+82+83+84+…+82014的和的个位数字是 .三、解答题
-
19. 计算: +(﹣1)2014﹣2sin45°+|﹣ |.20. 解不等式:4x﹣3>x+6,并把解集在数轴上表示出来.
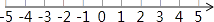 21. 在▱ABCD中,对角线AC、BD交于点O,过点O作直线EF分别交线段AD、BC于点E、F.(1)、根据题意,画出图形,并标上正确的字母;(2)、求证:DE=BF.22. 初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如图的统计图:
21. 在▱ABCD中,对角线AC、BD交于点O,过点O作直线EF分别交线段AD、BC于点E、F.(1)、根据题意,画出图形,并标上正确的字母;(2)、求证:DE=BF.22. 初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如图的统计图: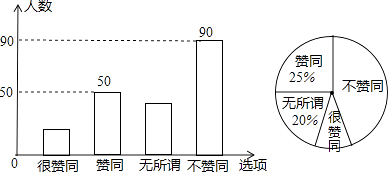 (1)、这次调查的家长总人数为人,表示“无所谓”的家长人数为人;(2)、随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是;(3)、求扇形统计图中表示“不赞同”的扇形的圆心角度数.23.
(1)、这次调查的家长总人数为人,表示“无所谓”的家长人数为人;(2)、随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是;(3)、求扇形统计图中表示“不赞同”的扇形的圆心角度数.23.中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
 (1)、沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(2)、由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: ≈1.414, ≈1.732)24. 电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.(1)、求该品牌电动自行车销售量的月均增长率;(2)、若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?25. 如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.
(1)、沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(2)、由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: ≈1.414, ≈1.732)24. 电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.(1)、求该品牌电动自行车销售量的月均增长率;(2)、若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?25. 如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.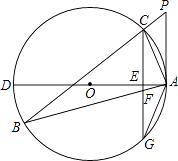 (1)、判断直线PA与⊙O的位置关系,并说明理由;(2)、求证:AG2=AF•AB;(3)、若⊙O的直径为10,AC=2 ,AB=4 ,求△AFG的面积.26.
(1)、判断直线PA与⊙O的位置关系,并说明理由;(2)、求证:AG2=AF•AB;(3)、若⊙O的直径为10,AC=2 ,AB=4 ,求△AFG的面积.26.如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
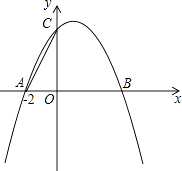 (1)、直接写出抛物线的解析式:;(2)、把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;(3)、除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
(1)、直接写出抛物线的解析式:;(2)、把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;(3)、除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.