2016-2017学年江苏省南通市启东市九年级下学期开学数学试卷
试卷更新日期:2017-04-25 类型:开学考试
一、选择题:
-
1. 抛物线y=(x+1)2+2的顶点( )A、(﹣1,2) B、(2,1) C、(1,2) D、(﹣1,﹣2)2. 如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
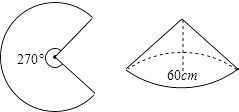 A、40cm B、50cm C、60cm D、80cm3. 如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )
A、40cm B、50cm C、60cm D、80cm3. 如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )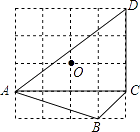 A、△ACD的外心 B、△ABC的外心 C、△ACD的内心 D、△ABC的内心4. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A、△ACD的外心 B、△ABC的外心 C、△ACD的内心 D、△ABC的内心4. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )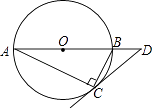 A、25° B、40° C、50° D、65°5. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A、25° B、40° C、50° D、65°5. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )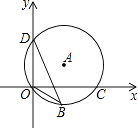 A、 B、 C、 D、6. 在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球6只,黑球4只,将袋中的球搅匀,闭上眼睛随机从袋中取出1只球,则取出黑球的概率是( )A、 B、 C、 D、7. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A、 B、 C、 D、6. 在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球6只,黑球4只,将袋中的球搅匀,闭上眼睛随机从袋中取出1只球,则取出黑球的概率是( )A、 B、 C、 D、7. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )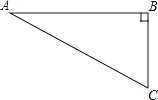 A、 B、 C、 D、8. 已知抛物线y=ax2+bx+c的图象如图所示,则|a﹣b+c|+|2a+b|=( )
A、 B、 C、 D、8. 已知抛物线y=ax2+bx+c的图象如图所示,则|a﹣b+c|+|2a+b|=( )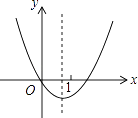 A、a+b B、a﹣2b C、a﹣b D、3a9. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A、a+b B、a﹣2b C、a﹣b D、3a9. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )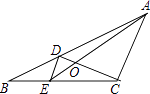 A、1:3 B、1:4 C、1:5 D、1:2510. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF . 其中正确的有( )
A、1:3 B、1:4 C、1:5 D、1:2510. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF . 其中正确的有( )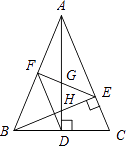 A、1个 B、2 个 C、3 个 D、4个
A、1个 B、2 个 C、3 个 D、4个二、填空题
-
11. “打开电视,正在播放《新闻联播》”是事件.12. 如图,点A为反比例函数y=﹣ 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为 .
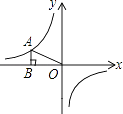 13. 抛物线y=2x2﹣2 x+1与坐标轴的交点个数是 .14. 如图,在⊙O中, ,∠AOB=40°,则∠ADC的度数是 .
13. 抛物线y=2x2﹣2 x+1与坐标轴的交点个数是 .14. 如图,在⊙O中, ,∠AOB=40°,则∠ADC的度数是 .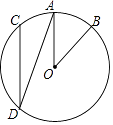 15. 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 .
15. 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 .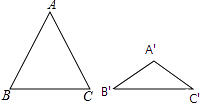 16. 如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为 .
16. 如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为 .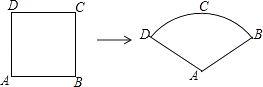 17. 有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2= .
17. 有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2= .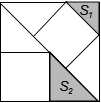 18. 如图,点A,B在反比例函数y= (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
18. 如图,点A,B在反比例函数y= (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .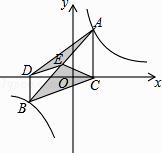
三、解答题
-
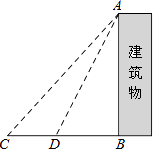
19. 计算:(﹣1)2016+2sin60°﹣|﹣ |+π0 .20. 某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ,tan48°≈ ,sin64°≈ ,tan64°≈2)
 21. 如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法)并说明理由.
21. 如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法)并说明理由.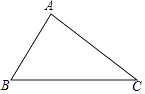 22.
22.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
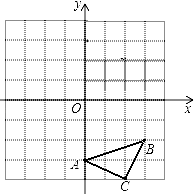 (1)、画出△ABC向上平移6个单位得到的△A1B1C1;(2)、以点C为位似中心,在网格中画出△A2B2C2 , 使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.23. 某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
(1)、画出△ABC向上平移6个单位得到的△A1B1C1;(2)、以点C为位似中心,在网格中画出△A2B2C2 , 使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.23. 某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:组号
分组
频数
一
6≤m<7
2
二
7≤m<8
7
三
8≤m<9
a
四
9≤m≤10
2
(1)、求a的值;(2)、若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;(3)、将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).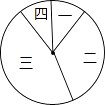 24. 如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
24. 如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.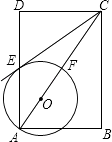 (1)、判断直线CE与⊙O的位置关系,并证明你的结论;(2)、若tan∠ACB= ,BC=2,求⊙O的半径.25. 如图,一次函数y=x+m的图象与反比例函数y= 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
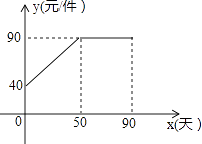
(1)、判断直线CE与⊙O的位置关系,并证明你的结论;(2)、若tan∠ACB= ,BC=2,求⊙O的半径.25. 如图,一次函数y=x+m的图象与反比例函数y= 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).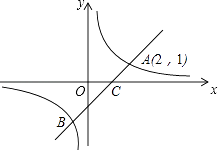 (1)、求m及k的值;(2)、求点C的坐标,并结合图象写出不等式组0<x+m≤ 的解集.26. 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
(1)、求m及k的值;(2)、求点C的坐标,并结合图象写出不等式组0<x+m≤ 的解集.26. 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).时间x(天)
1
30
60
90
每天销售量p(件)
198
140
80
20
 (1)、求出w与x的函数关系式;(2)、问销售该商品第几天时,当天的销售利润最大?并求出最大利润;(3)、该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.27. 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)、求出w与x的函数关系式;(2)、问销售该商品第几天时,当天的销售利润最大?并求出最大利润;(3)、该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.27. 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO. (1)、已知BD= ,求正方形ABCD的边长;(2)、猜想线段EM与CN的数量关系并加以证明.28. 如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)、已知BD= ,求正方形ABCD的边长;(2)、猜想线段EM与CN的数量关系并加以证明.28. 如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.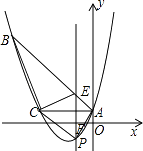 (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.