2014年广西防城港市中考数学试卷
试卷更新日期:2017-04-25 类型:中考真卷
一、单项选择题
-
1. 下面的数中,与﹣2的和为0的是( )A、2 B、﹣2 C、 D、-2. 将6.18×10﹣3化为小数的是( )A、0.000618 B、0.00618 C、0.0618 D、0.6183. 计算(2a2)3的结果是( )A、2a6 B、6a6 C、8a6 D、8a54. 下面的多项式在实数范围内能因式分解的是( )A、x2+y2 B、x2﹣y C、x2+x+1 D、x2﹣2x+15. 如图的几何体的三视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 下列命题是假命题的是( )A、四个角相等的四边形是矩形 B、对角线相等的平行四边形是矩形 C、对角线垂直的四边形是菱形 D、对角线垂直的平行四边形是菱形7. △ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )A、3 B、6 C、9 D、128. 一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、9. x1 , x2是关于x的一元二次方程x2﹣mx+m﹣2=0的两个实数根,是否存在实数m使 + =0成立?则正确的结论是( )A、m=0时成立 B、m=2时成立 C、m=0或2时成立 D、不存在10. 在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )A、1cm<AB<4cm B、5cm<AB<10cm C、4cm<AB<8cm D、4cm<AB<10cm11. 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( )
6. 下列命题是假命题的是( )A、四个角相等的四边形是矩形 B、对角线相等的平行四边形是矩形 C、对角线垂直的四边形是菱形 D、对角线垂直的平行四边形是菱形7. △ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )A、3 B、6 C、9 D、128. 一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、9. x1 , x2是关于x的一元二次方程x2﹣mx+m﹣2=0的两个实数根,是否存在实数m使 + =0成立?则正确的结论是( )A、m=0时成立 B、m=2时成立 C、m=0或2时成立 D、不存在10. 在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )A、1cm<AB<4cm B、5cm<AB<10cm C、4cm<AB<8cm D、4cm<AB<10cm11. 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( ) A、4个 B、6个 C、8个 D、10个12.
A、4个 B、6个 C、8个 D、10个12.如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
 A、
A、 B、
B、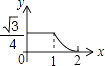 C、
C、 D、
D、
二、填空题
-
13. 3的倒数是 .14. 在平面直角坐标系中,点(﹣4,4)在第象限.15. 下表是我市某一天在不同时段测得的气温情况
0:00
4:00
8:00
12:00
16:00
20:00
25℃
27℃
29℃
32℃
34℃
30℃
则这一天气温的极差是℃.
16. 如图,直线MN与⊙O相切于点M,ME=EF且EF∥MN,则cos∠E= . 17. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,∠A=120°,AD=2,BD平分∠ABC,则梯形ABCD的周长是 .
17. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,∠A=120°,AD=2,BD平分∠ABC,则梯形ABCD的周长是 . 18.
18.如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= 和y= 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
① = ;
②阴影部分面积是 (k1+k2);
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.

其中正确的结论是(把所有正确的结论的序号都填上).
三、解答题
-
19. 计算:(﹣2)2﹣ • +(sin60°﹣π)0 .
20. 先化简,再求值: ﹣ ,其中x= ﹣1.21.如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是 .
 22. 第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题:
22. 第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题: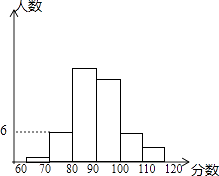 (1)、全班学生是多少人?(2)、成绩不少于90分为优秀,那么全班成绩的优秀率是多少?(3)、若不少于100分可以得到A+等级,则小明得到A+的概率是多少?23. 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)、全班学生是多少人?(2)、成绩不少于90分为优秀,那么全班成绩的优秀率是多少?(3)、若不少于100分可以得到A+等级,则小明得到A+的概率是多少?23. 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E. (1)、求证:∠1=∠2.(2)、已知:OF:OB=1:3,⊙O的半径为3,求AG的长.24. 我市市区去年年底电动车拥有量是10万辆,为了缓解城区交通拥堵状况,今年年初,市交通部门要求我市到明年年底控制电动车拥有量不超过11.9万辆,估计每年报废的电动车数量是上一年年底电动车拥有量的10%,假定每年新增电动车数量相同,问:(1)、从今年年初起每年新增电动车数量最多是多少万辆?(2)、在(1)的结论下,今年年底到明年年底电动车拥有量的年增长率是多少?(结果精确到0.1%)25. 如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)、求证:∠1=∠2.(2)、已知:OF:OB=1:3,⊙O的半径为3,求AG的长.24. 我市市区去年年底电动车拥有量是10万辆,为了缓解城区交通拥堵状况,今年年初,市交通部门要求我市到明年年底控制电动车拥有量不超过11.9万辆,估计每年报废的电动车数量是上一年年底电动车拥有量的10%,假定每年新增电动车数量相同,问:(1)、从今年年初起每年新增电动车数量最多是多少万辆?(2)、在(1)的结论下,今年年底到明年年底电动车拥有量的年增长率是多少?(结果精确到0.1%)25. 如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP. (1)、求证:四边形BMNP是平行四边形;(2)、线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.26.
(1)、求证:四边形BMNP是平行四边形;(2)、线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.26.给定直线l:y=kx,抛物线C:y=ax2+bx+1.
 (1)、当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;(2)、若把直线l向上平移k2+1个单位长度得到直线l′,则无论非零实数k取何值,直线l′与抛物线C都只有一个交点.
(1)、当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;(2)、若把直线l向上平移k2+1个单位长度得到直线l′,则无论非零实数k取何值,直线l′与抛物线C都只有一个交点.①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.