2014年广西崇左市中考数学试卷

试卷更新日期：2017-04-25 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列实数是无理数的是（）

A、 $\sqrt{2}$ B、1 C、0 D、﹣1

查看试题解析
2. 如图，直线AB∥CD，如果∠1=70°，那么∠BOF的度数是（）

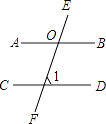A、70° B、100° C、110° D、120°

查看试题解析
3. 震惊世界的MH370失联事件发生后第30天，中国“海巡01”轮在南印度洋海域搜索过程中，首次侦听到疑是飞机黑匣子的脉冲信号，探测到的信号所在海域水深4500米左右，其中4500用科学记数法表示为（）

A、4.5×10² B、4.5×10³ C、45.0×10² D、0.45×10⁴

查看试题解析
4. 在2014年5月崇左市教育局举行的“经典诗朗诵”演讲比赛中，有11名学生参加决赛，他们决赛的成绩各不相同，其中的一名学生想知道自己能否进入前6名，不仅要了解自己的成绩，还要了解这11名学生成绩的（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
5. 下列几何体的主视图、左视图、俯视图的图形完全相同的是（）

A、三棱锥 B、长方体 C、三棱柱 D、球体

查看试题解析
6. 如果崇左市市区某中午的气温是37℃，到下午下降了3℃，那么下午的气温是（）

A、40℃ B、38℃ C、36℃ D、34℃

查看试题解析
7. 若点A（2，4）在函数y=kx的图象上，则下列各点在此函数图象上的是（）

A、（1，2） B、（﹣2，﹣1） C、（﹣1，2） D、（2，﹣4）

查看试题解析
8. 下列说法正确的是（）

A、对角线相等的平行四边形是菱形 B、有一组邻边相等的平行四边形是菱形 C、对角线相互垂直的四边形是菱形 D、有一个角是直角的平行四边形是菱形

查看试题解析
9. 方程组 ${\begin{matrix} x + y = 60 \\ x - 2 y = 30 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 70 \\ y = - 10 \end{matrix}$ B、 ${\begin{matrix} x = 90 \\ y = - 30 \end{matrix}$ C、 ${\begin{matrix} x = 50 \\ y = 10 \end{matrix}$ D、 ${\begin{matrix} x = 30 \\ y = 30 \end{matrix}$

查看试题解析
10. 已知点A（a，2013）与点B（2014，b）关于x轴对称，则a+b的值为（）

A、﹣1 B、1 C、2 D、3

查看试题解析
11. 如图，下面是利用尺规作∠AOB的角平分线OC的作法，在用尺规作角平分线过程中，用到的三角形全等的判定方法是（）
作法：
①以O为圆心，适当长为半径画弧，分别交OA，OB于点D，E；
②分别以D，E为圆心，大于 $\frac{1}{2}$ DE的长为半径画弧，两弧在∠AOB内交于一点C；
③画射线OC，射线OC就是∠AOB的角平分线．

A、ASA B、SAS C、SSS D、AAS

查看试题解析
12.
如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2）．把一条长为2014个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（）

A、（﹣1，0） B、（1，﹣2） C、（1，1） D、（﹣1，﹣1）

查看试题解析

二、填空题

13. 若分式 $\frac{x - 2}{x}$ 的值是0，则x的值为．

查看试题解析
14. 因式分解：x²﹣1= ．

查看试题解析
15. 化简： $\frac{a^{2} b + a b^{2}}{2 a^{2} b^{2}}$ = $\frac{()}{2 a b}$ ．．

查看试题解析
16. 已知在一个样本中，50个数据分别落在5个组内，第一，二，三，四，五组数据的个数分别是2，8，15，20，5，则第四组频数为．

查看试题解析
17. 已知直角三角形的两条直角边长为6，8，那么斜边上的中线长是．

查看试题解析
18. 如图，A（4，0），B（3，3），以AO，AB为边作平行四边形OABC，则经过C点的反比例函数的解析式为．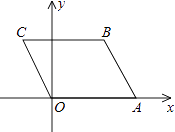

查看试题解析

三、解答题

19. 计算：（ $\frac{1}{2}$ ）^﹣¹﹣2014⁰﹣2sin30°+ $\sqrt{8}$ ．

查看试题解析
20. 解不等式2x﹣3＜ $\frac{x + 1}{3}$ ，并把解集在数轴上表示出来．

查看试题解析
21. 写出下列命题的已知、求证，并完成证明过程．

(1)、
命题：如果一个三角形的两个角相等，那么这两个角所对的边也相等（简称：“等角对等边”）．

已知：如图，．
求证：．

(2)、证明命题

查看试题解析
22. 如图，在四边形ABCD中，对角线AC，BD相交于点O，且AC⊥BD，点E，F，G，H分别是AB，BC，CD，DA的中点，依次连接各边中点得到四边形EFGH，求证：四边形EFGH是矩形．

查看试题解析
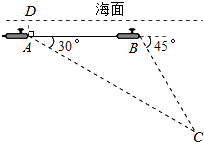
23.
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米．如图，某天该深潜器在海面下2000米的A点处作业，测得俯角为30°正前方的海底C点处有黑匣子信号发出．该深潜器受外力作用可继续在同一深度直线航行3000米后，再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出，请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子．（参考数据 $\sqrt{3}$ ≈1.732）

查看试题解析
24. 在一个不透明的布袋里装有4个标有1，2，3，4的小球，它们的形状、大小、质地完全相同，小李从布袋里随机取出一个小球，记下数字为x，小张在剩下的3个小球中随机取出一个小球，记下数字为y，这样确定了点Q的坐标（x，y）．

(1)、画树状图或列表，写出点Q所有可能的坐标；

(2)、求点Q（x，y）在函数y=﹣x+5图象上的概率．

查看试题解析
25. 如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=1，ED=2．

(1)、求证：∠ABC=∠D；

(2)、求AB的长；

(3)、延长DB到F，使得BF=BO，连接FA，试判断直线FA与⊙O的位置关系，并说明理由．

查看试题解析
26.
在平面直角坐标系中，一次函数y=kx+b的图象与x轴、y轴分别相交于A（﹣3，0），B（0，﹣3）两点，二次函数y=x²+mx+n的图象经过点A．

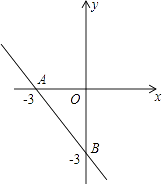(1)、求一次函数y=kx+b的解析式；

(2)、若二次函数y=x²+mx+n图象的顶点在直线AB上，求m，n的值；

(3)、当﹣3≤x≤0时，二次函数y=x²+mx+n的最小值为﹣4，求m，n的值．

查看试题解析