2014年广西百色市中考数学试卷

试卷更新日期：2017-04-25 类型：中考真卷

进入出卷网下载

一、单项选择题

1. 化简 $\sqrt{100}$ 得（）

A、100 B、10 C、 $\sqrt{10}$ D、±10

查看试题解析
2. 下列图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，已知AB∥CD，∠1=62°，则∠2的度数是（）

A、28° B、62° C、108° D、118°

查看试题解析
4. 在3月份，某县某一周七天的最高气温（单位：℃）分别为：12，9，10，6，11，12，17，则这组数据的极差是（）

A、6 B、11 C、12 D、17

查看试题解析
5. 下列式子正确的是（）

A、（a﹣b）²=a²﹣2ab+b² B、（a﹣b）²=a²﹣b² C、（a﹣b）²=a²+2ab+b² D、（a﹣b）²=a²﹣ab+b²

查看试题解析
6. 下列几何体中，同一个几何体的主视图与俯视图不同的是（）

A、圆柱 B、正方体 C、圆锥 D、球

查看试题解析
7. 已知x=2是一元二次方程x²﹣2mx+4=0的一个解，则m的值为（）

A、2 B、0 C、0或2 D、0或﹣2

查看试题解析
8. 下列三个分式 $\frac{1}{2 x^{2}}$ 、 $\frac{5 x - 1}{4 (m - n)}$ 、 $\frac{3}{x}$ 的最简公分母是（）

A、4（m﹣n）x B、2（m﹣n）x² C、 $\frac{1}{4 x^{2} (m - n)}$ D、4（m﹣n）x²

查看试题解析
9. 某班第一组12名同学在“爱心捐款”活动中，捐款情况统计如下表，则捐款数组成的一组数据中，中位数与众数分别是（）
捐款（元）
10
15
20
50
人数
1
5
4
2

A、15，15 B、17.5，15 C、20，20 D、15，20

查看试题解析
10.
从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（）

A、（6+6 $\sqrt{3}$ ）米 B、（6+3 $\sqrt{3}$ ）米 C、（6+2 $\sqrt{3}$ ）米 D、12米

查看试题解析
11. 在下列叙述中：

①一组对边相等的四边形是平行四边形；
②函数y= $\frac{2}{x}$ 中，y随x的增大而减小；
③有一组邻边相等的平行四边形是菱形；
④有不可能事件A发生的概率为0.0001．
正确的叙述有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
12. 已知点A的坐标为（2，0），点P在直线y=x上运动，当以点P为圆心，PA的长为半径的圆的面积最小时，点P的坐标为（）

A、（1，﹣1） B、（0，0） C、（1，1） D、（ $\sqrt{2}$ ， $\sqrt{2}$ ）

查看试题解析

二、填空题

13. 计算：2000﹣2015= ．

查看试题解析
14. 已知甲、乙两组抽样数据的方差： $S_{甲}^{2}$ =95.43， $S_{乙}^{2}$ =5.32，可估计总体数据比较稳定的是组数据．

查看试题解析
15. 如图，AB是⊙O的直径，点C为⊙O上一点，∠AOC=50°，则∠ABC= ．

查看试题解析
16. 方程组 ${\begin{matrix} x + y = 0 \\ x - y = 2 \end{matrix}$ 的解为．

查看试题解析
17. 如图，在△ABC中，AC=BC，∠B=70°，分别以点A、C为圆心，大于 $\frac{1}{2}$ AC的长为半径作弧，两弧相交于点M、N，作直线MN，分别交AC、BC于点D、E，连结AE，则∠AED的度数是°．

查看试题解析
18. 观察以下等式：3²﹣1²=8，5²﹣1²=24，7²﹣1²=48，9²﹣1²=80，…由以上规律可以得出第n个等式为．

查看试题解析

三、解答题

19. 计算：（π﹣3.14）⁰+（﹣1）²⁰¹⁵+|1﹣ $\sqrt{3}$ |﹣3tan30°．

查看试题解析
20. 当a=2014时，求 $\frac{a^{2} + 2 a}{a - 1}$ ÷（a+ $\frac{a}{a - 1}$ ）的值．

查看试题解析
21. 如图，在边为的1正方形组成的网格中，建立平面直角坐标系，若A（﹣4，2）、B（﹣2，3）、C（﹣1，1），将△ABC沿着x轴翻折后，得到△DEF，点B的对称点是点E，求过点E的反比例函数解析式，并写出第三象限内该反比例函数图象所经过的所有格点的坐标．

查看试题解析
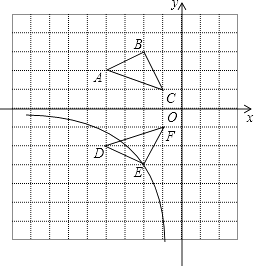22. 如图，已知点E、F在四边形ABCD的对角线延长线上，AE=CF，DE∥BF，∠1=∠2．

(1)、求证：△AED≌△CFB；

(2)、若AD⊥CD，四边形ABCD是什么特殊四边形？请说明理由．

查看试题解析
23. 学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况，所得数据用表格与条形图描述如下：
科目
语文
数学
英语
体育
音乐
人数
10
a
15
3
2

(1)、表格中a的值为；

(2)、补全条形图；

(3)、小李是最喜欢体育之一，小张是最喜欢音乐之一，计划从最喜欢体育、音乐的人中，每科目各选1人参加学校训练，用列表或树形图表示所有结果，并求小李、小张至少有1人被选上的概率是多少？

查看试题解析
24. 有2条生产线计划在一个月（30天）内组装520台产品（每天产品的产量相同），按原先的组装速度，不能完成任务；若加班生产，每条生产线每天多组装2台产品，能提前完成任务．

(1)、每条生产线原先每天最多能组装多少台产品？

(2)、要按计划完成任务，策略一：增添1条生产线，共要多投资19000元；策略二：按每天能组装最多台数加班生产，每条生产线每天共要多花费350元；选哪一个策略较省费用？

查看试题解析
25. 如图，在正方形ABCD中，点E、F分别是BC、CD的中点，DE交AF于点M，点N为DE的中点．

(1)、若AB=4，求△DNF的周长及sin∠DAF的值；

(2)、求证：2AD•NF=DE•DM．

查看试题解析
26. 已知过原点O的两直线与圆心为M（0，4），半径为2的圆相切，切点分别为P、Q，PQ交y轴于点K，抛物线经过P、Q两点，顶点为N（0，6），且与x轴交于A、B两点．

(1)、求点P的坐标；

(2)、求抛物线解析式；

(3)、在直线y=nx+m中，当n=0，m≠0时，y=m是平行于x轴的直线，设直线y=m与抛物线相交于点C、D，当该直线与⊙M相切时，求点A、B、C、D围成的多边形的面积（结果保留根号）．

查看试题解析

捐款（元）	10	15	20	50
人数	1	5	4	2

科目	语文	数学	英语	体育	音乐
人数	10	a	15	3	2