2014年广东省深圳市中考数学试卷

试卷更新日期：2017-04-25 类型：中考真卷

进入出卷网下载

一、选择题

1. 9的相反数是（）

A、﹣9 B、9 C、±9 D、 $\frac{1}{9}$

查看试题解析
2. 下列图形中是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 支付宝与“快的打车”联合推出优惠，“快的打车”一夜之间红遍大江南北．据统计，2014年“快的打车”账户流水总金额达到47.3亿元，47.3亿用科学记数法表示为（）

A、4.73×10⁸ B、4.73×10⁹ C、4.73×10¹⁰ D、4.73×10¹¹

查看试题解析
4. 由几个大小相同的正方形组成的几何图形如图，则它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 在﹣2，1，2，1，4，6中正确的是（）

A、平均数3 B、众数是﹣2 C、中位数是1 D、极差为8

查看试题解析
6. 已知函数y=ax+b经过（1，3），（0，﹣2），则a﹣b=（）

A、﹣1 B、﹣3 C、3 D、7

查看试题解析
7. 下列方程没有实数根的是（）

A、x²+4x=10 B、3x²+8x﹣3=0 C、x²﹣2x+3=0 D、（x﹣2）（x﹣3）=12

查看试题解析
8. 如图，△ABC和△DEF中，AB=DE、∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（）

A、AC∥DF B、∠A=∠D C、AC=DF D、∠ACB=∠F

查看试题解析
9. 袋子里有4个球，标有2，3，4，5，先抽取一个并记住，放回，然后再抽取一个，所抽取的两个球数字之和大于6的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{7}{12}$ C、 $\frac{5}{8}$ D、 $\frac{3}{4}$

查看试题解析
10.
小明去爬山，在山脚看山顶角度为30°，小明在坡比为5：12的山坡上走1300米，此时小明看山顶的角度为60°，求山高（）

A、600﹣250 $\sqrt{5}$ 米 B、600 $\sqrt{3}$ ﹣250米 C、350+350 $\sqrt{3}$ 米 D、500 $\sqrt{3}$ 米

查看试题解析
11.
二次函数y=ax²+bx+c图象如图，下列正确的个数为（）

①bc＞0；
②2a﹣3c＜0；
③2a+b＞0；
④ax²+bx+c=0有两个解x₁ ， x₂ ，当x₁＞x₂时，x₁＞0，x₂＜0；
⑤a+b+c＞0；
⑥当x＞1时，y随x增大而减小．

A、2 B、3 C、4 D、5

查看试题解析
12. 如图，已知四边形ABCD为等腰梯形，AD∥BC，AB=CD，AD= $\sqrt{2}$ ，E为CD中点，连接AE，且AE=2 $\sqrt{3}$ ，∠DAE=30°，作AE⊥AF交BC于F，则BF=（）

A、1 B、3﹣ $\sqrt{3}$ C、 $\sqrt{5}$ ﹣1 D、4﹣2 $\sqrt{2}$

查看试题解析

二、填空题

13. 分解因式：2x²﹣8= ．

查看试题解析
14. 在Rt△ABC中，∠C=90°，AD平分∠CAB，AC=6，BC=8，CD= ．

查看试题解析
15. 如图，双曲线y= $\frac{k}{x}$ 经过Rt△BOC斜边上的点A，且满足 $\frac{A O}{A B}$ = $\frac{2}{3}$ ，与BC交于点D，S_△_BOD=21，求k= ．

查看试题解析
16.
如图，下列图形是将正三角形按一定规律排列，则第5个图形中所有正三角形的个数有．

查看试题解析

三、解答题

17. 计算： $\sqrt{12}$ ﹣2tan60°+（ $\sqrt{2014}$ ﹣1）⁰﹣（ $\frac{1}{3}$ ）^﹣¹ ．

查看试题解析
18. 先化简，再求值：（ $\frac{3 x}{x - 2}$ ﹣ $\frac{x}{x + 2}$ ）÷ $\frac{x}{x^{2} - 4}$ ，在﹣2，0，1，2四个数中选一个合适的代入求值．

查看试题解析
19. 关于体育选考项目统计图
项目
频数
频率
A
80
b
B
c
0.3
C
20
0.1
D
40
0.2
合计
a
1

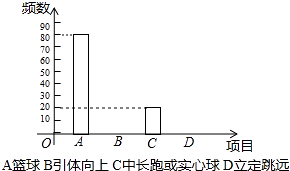(1)、求出表中a，b，c的值，并将条形统计图补充完整．
表中a= ， b= ， c= ．

(2)、如果有3万人参加体育选考，会有多少人选择篮球？

查看试题解析
20. 已知BD垂直平分AC，∠BCD=∠ADF，AF⊥AC，

(1)、证明四边形ABDF是平行四边形；

(2)、若AF=DF=5，AD=6，求AC的长．

查看试题解析
21. 某“爱心义卖”活动中，购进甲、乙两种文具，甲每个进货价高于乙进货价10元，90元买乙的数量与150元买甲的数量相同．

(1)、求甲、乙进货价；

(2)、甲、乙共100件，将进价提高20%进行销售，进货价少于2080元，销售额要大于2460元，求有几种方案？

查看试题解析
22. 如图，在平面直角坐标系中，⊙M过原点O，与x轴交于A（4，0），与y轴交于B（0，3），点C为劣弧AO的中点，连接AC并延长到D，使DC=4CA，连接BD．

(1)、求⊙M的半径；

(2)、证明：BD为⊙M的切线；

(3)、在直线MC上找一点P，使|DP﹣AP|最大．

查看试题解析
23.
如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，﹣4）．

(1)、求抛物线的解析式；

(2)、将抛物线顶点沿着直线AB平移，此时顶点记为E，与y轴的交点记为F，
①求当△BEF与△BAO相似时，E点坐标；
②记平移后抛物线与AB另一个交点为G，则S_△_EFG与S_△_ACD是否存在8倍的关系？若有请直接写出F点的坐标．

查看试题解析

项目	频数	频率
A	80	b
B	c	0.3
C	20	0.1
D	40	0.2
合计	a	1