2013年广东省湛江市中考数学试卷
试卷更新日期:2017-04-25 类型:中考真卷
一、选择题:
-
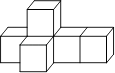
1. 下列各数中,最小的数是( )A、1 B、 C、0 D、﹣12. 国家提倡“低碳减排”,湛江某公司计划在海边建风能发电站,电站年均发电量约为213000000度,若将数据213000000用科学记数法表示为( )A、213×106 B、21.3×107 C、2.13×108 D、2.13×1093. 气候宜人的省级度假胜地吴川吉兆,测得一至五月份的平均气温分别为17、17、20、22、24(单位:℃),这组数据的中位数是( )A、24 B、22 C、20 D、174. 如图是由6个大小相同的正方体组成的几何体,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形6. 在平面直角坐标系中,点A(2,﹣3)在第 象限.( )A、一 B、二 C、三 D、四7. 下列运算正确的是( )A、a2•a3=a6 B、(a2)4=a6 C、a4÷a=a3 D、(x+y)2=x2+y28. 函数y= 中,自变量x的取值范围是( )A、x>﹣3 B、x≥﹣3 C、x≠﹣3 D、x≤﹣39. 计算 的结果是( )A、0 B、1 C、﹣1 D、x10. 由于受H7N9禽流感的影响,今年4月份鸡的价格两次大幅下降.由原来每斤12元连续两次降价a%后售价下调到每斤5元,下列所列方程中正确的是( )A、12(1+a%)2=5 B、12(1﹣a%)2=5 C、12(1﹣2a%)=5 D、12(1﹣a2%)=511. 如图,AB是⊙O的直径,∠AOC=110°,则∠D=( )
5. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形6. 在平面直角坐标系中,点A(2,﹣3)在第 象限.( )A、一 B、二 C、三 D、四7. 下列运算正确的是( )A、a2•a3=a6 B、(a2)4=a6 C、a4÷a=a3 D、(x+y)2=x2+y28. 函数y= 中,自变量x的取值范围是( )A、x>﹣3 B、x≥﹣3 C、x≠﹣3 D、x≤﹣39. 计算 的结果是( )A、0 B、1 C、﹣1 D、x10. 由于受H7N9禽流感的影响,今年4月份鸡的价格两次大幅下降.由原来每斤12元连续两次降价a%后售价下调到每斤5元,下列所列方程中正确的是( )A、12(1+a%)2=5 B、12(1﹣a%)2=5 C、12(1﹣2a%)=5 D、12(1﹣a2%)=511. 如图,AB是⊙O的直径,∠AOC=110°,则∠D=( )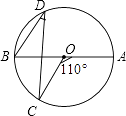 A、25° B、35° C、55° D、70°12. 四张质地、大小相同的卡片上,分别画上如图所示的四个图形.在看不到图形的情况下从中任意抽取一张,则抽取的卡片是轴对称图形的概率为( )
A、25° B、35° C、55° D、70°12. 四张质地、大小相同的卡片上,分别画上如图所示的四个图形.在看不到图形的情况下从中任意抽取一张,则抽取的卡片是轴对称图形的概率为( )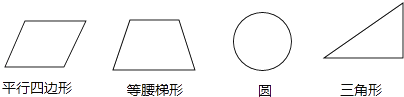 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题:
-
13. 分解因式:x2﹣4= .14. 抛物线y=x2+1的最小值是 .15. 若反比例函数y= 的图象经过点A(1,2),则k= .16.
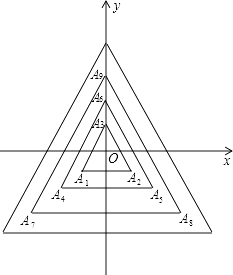
如图,所有正三角形的一边平行于x轴,一顶点在y轴上.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A3的坐标是 , A92的坐标是 .
三、解答题
-
17. 计算:|﹣6|﹣ ﹣(﹣1)2 .18. 解不等式组 ,并把它的解集在数轴上表示出来.
 19. 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
19. 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.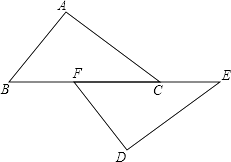 20. 把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.(1)、试求取出的两张卡片数字之和为奇数的概率;(2)、若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.21.
20. 把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.(1)、试求取出的两张卡片数字之和为奇数的概率;(2)、若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.21.如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位,其中 =1.732)
 22. 2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
22. 2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:频率分布表
分数段
频数
频率
50.5﹣60.5
16
0.08
60.5﹣70.5
40
0.2
70.5﹣80.5
50
0.25
80.5﹣90.5
m
0.35
90.5﹣100.5
24
n
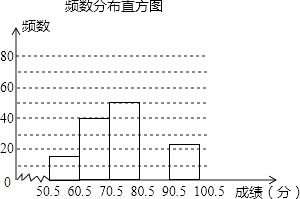 (1)、这次抽取了名学生的竞赛成绩进行统计,其中:m= , n=;(2)、补全频数分布直方图;(3)、若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?23. 如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
(1)、这次抽取了名学生的竞赛成绩进行统计,其中:m= , n=;(2)、补全频数分布直方图;(3)、若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?23. 如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC. (1)、求证:PA为⊙O的切线;(2)、若OB=5,OP= ,求AC的长.24. 阅读下面的材料,先完成阅读填空,再按要求答题:
(1)、求证:PA为⊙O的切线;(2)、若OB=5,OP= ,求AC的长.24. 阅读下面的材料,先完成阅读填空,再按要求答题:
(1)、阅读填空sin30°= ,cos30°= ,则sin230°+cos230°= ;①
sin45°= ,cos45°= ,则sin245°+cos245°= ;②
sin60°= ,cos60°= ,则sin260°+cos260°= .③
…
观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A= .④
(2)、如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理对∠A证明你的猜想;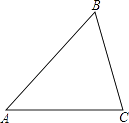 (3)、已知:∠A为锐角(cosA>0)且sinA= ,求cosA.
(3)、已知:∠A为锐角(cosA>0)且sinA= ,求cosA.
25. 周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟后,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象. (1)、求小明骑车的速度和在南亚所游玩的时间;(2)、若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.26.
(1)、求小明骑车的速度和在南亚所游玩的时间;(2)、若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.26.如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5).
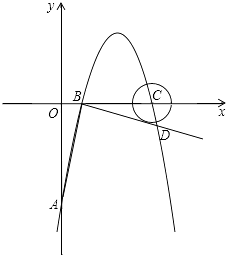 (1)、求此抛物线的解析式;(2)、过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;(3)、在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求此抛物线的解析式;(2)、过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;(3)、在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.