2013年广东省茂名市中考数学试卷

试卷更新日期：2017-04-25 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列实数中，最小的数是（）

A、﹣3 B、3 C、 $\frac{1}{3}$ D、0

查看试题解析
2. 下列食品商标中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各式由左边到右边的变形中，属于分解因式的是（）

A、a（x+y）=ax+ay B、x²﹣4x+4=x（x﹣4）+4 C、10x²﹣5x=5x（2x﹣1） D、x²﹣16+6x=（x+4）（x﹣4）+6x

查看试题解析
4. 下列事件中为必然事件的是（）

A、打开电视机，正在播放茂名新闻 B、早晨的太阳从东方升起 C、随机掷一枚硬币，落地后正面朝上 D、下雨后，天空出现彩虹

查看试题解析
5. 如图，由两个相同的正方体和一个圆锥体组成一个立体图形，其俯视图是（）

A、 B、 C、 D、

查看试题解析
6. PM2.5是指大气中直径小于或等于2.5μm（0.0000025m）的颗粒物，含有大量有毒、有害物质，也称可入肺颗粒物．将0.0000025用科学记数法表示为（）

A、25×10^﹣⁷ B、2.5×10^﹣⁶ C、0.25×10^﹣⁵ D、2.5×10⁶

查看试题解析
7. 商店某天销售了13双运动鞋，其尺码统计如下表：
尺码（单位：码）
38
39
40
41
42
数量（单位：双）
2
5
3
1
2
则这13双运动鞋尺码的众数和中位数分别是（）

A、39码、39码 B、39码、40码 C、40码、39码 D、40码、40码

查看试题解析
8. 如图，矩形ABCD的两条对角线相交于点O，∠AOD=60°，AD=2，则AC的长是（）

A、2 B、4 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
9. 下列二次函数的图象，不能通过函数y=3x²的图象平移得到的是（）

A、y=3x²+2 B、y=3（x﹣1）² C、y=3（x﹣1）²+2 D、y=2x²

查看试题解析
10. 如图，小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上，并测得∠1=25°，则∠2的度数是（）

A、15° B、25° C、35° D、45°

查看试题解析

二、填空题

11. 计算：3 $\sqrt{2}$ ﹣2 $\sqrt{2}$ = ．

查看试题解析
12.
小李和小林练习射箭，射完10箭后两人的成绩如图所示，通常新手的成绩不太稳定，根据图中的信息，估计这两人中的新手是．

查看试题解析
13. 如图，四条直径把两个同心圆分成八等份，若往圆面投掷飞镖，则飞镖落在白色区域的概率是．

查看试题解析
14. 如图是李大妈跳舞用的扇子，这个扇形AOB的圆心角∠O=120°，半径OA=3，则弧AB的长度为（结果保留π）．

查看试题解析
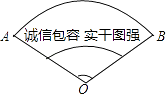15.
如图，三个正比例函数的图象分别对应表达式：①y=ax，②y=bx，③y=cx，将a，b，c从小到大排列并用“＜”连接为．

查看试题解析

三、用心做一做

16. 先化简，后求值：a²•a⁴﹣a⁸÷a²+（a³）² ，其中a=﹣1．

查看试题解析
17. 解分式方程： $\frac{3}{x - 1} = \frac{4}{x}$ ．

查看试题解析
18. 在格纸上按以下要求作图，不用写作法：

(1)、作出“小旗子”向右平移6格后的图案；

(2)、作出“小旗子”绕O点按逆时针方向旋转90°后的图案．

查看试题解析

四、沉着冷静，缜密思考

19. 在某校举行的“中国学生营养日”活动中，设计了抽奖环节：在一只不透明的箱子中有3个球，其中2个红球，1个白球，它们除颜色外均相同．

(1)、随机摸出一个球，恰好是红球就能中奖，则中奖的概率是多少？

(2)、同时摸出两个球，都是红球就能中特别奖，则中特别奖的概率是多少？（要求画树状图或列表求解）

查看试题解析
20. 当前，“校园手机”现象已经受到社会广泛关注，某数学兴趣小组对“是否赞成中学生带手机进校园”的问题进行了社会调查．小文将调查数据作出如下不完整的整理：
频数分布表
看法
频数
频率
赞成
5
无所谓
0.1
反对
40
0.8

(1)、请求出共调查了多少人；并把小文整理的图表补充完整；

(2)、小丽要将调查数据绘制成扇形统计图，则扇形图中“赞成”的圆心角是多少度？

查看试题解析

五、满怀信心，再接再厉

21. 如图，在▱ABCD中，点E是AB边的中点，DE与CB的延长线交于点F．

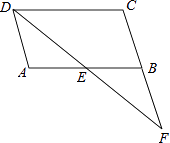(1)、求证：△ADE≌△BFE；

(2)、若DF平分∠ADC，连接CE．试判断CE和DF的位置关系，并说明理由．

查看试题解析
22. 如图，反比例函数 $y = \frac{6}{x}$ 的图象与一次函数y=kx+b的图象相交于两点A（m，3）和B（﹣3，n）．

(1)、求一次函数的表达式；

(2)、观察图象，直接写出使反比例函数值大于一次函数值的自变量x的取值范围．

查看试题解析
23. 在信宜市某“三华李”种植基地有A、B两个品种的树苗出售，已知A种比B种每株多2元，买1株A种树苗和2株B种树苗共需20元．

(1)、问A、B两种树苗每株分别是多少元？

(2)、为扩大种植，某农户准备购买A、B两种树苗共360株，且A种树苗数量不少于B种数量的一半，请求出费用最省的购买方案．

查看试题解析

六、灵动智慧，超越自我

24. 如图，在⊙O中，弦AB与弦CD相交于点G，OA⊥CD于点E，过点B的直线与CD的延长线交于点F，AC∥BF．

(1)、若∠FGB=∠FBG，求证：BF是⊙O的切线；

(2)、若tan∠F= $\frac{3}{4}$ ，CD=a，请用a表示⊙O的半径；

(3)、求证：GF²﹣GB²=DF•GF．

查看试题解析
25.
如图，抛物线 $y = a x^{2} - \frac{1}{3} x + 2$ 与x轴交于点A和点B，与y轴交于点C，已知点B的坐标为（3，0）．

(1)、求a的值和抛物线的顶点坐标；

(2)、分别连接AC、BC．在x轴下方的抛物线上求一点M，使△AMC与△ABC的面积相等；

(3)、设N是抛物线对称轴上的一个动点，d=|AN﹣CN|．探究：是否存在一点N，使d的值最大？若存在，请直接写出点N的坐标和d的最大值；若不存在，请简单说明理由．

查看试题解析

尺码（单位：码）	38	39	40	41	42
数量（单位：双）	2	5	3	1	2

看法	频数	频率
赞成	5
无所谓		0.1
反对	40	0.8