2012年广东省茂名市中考数学试卷

试卷更新日期：2017-04-25 类型：中考真卷

进入出卷网下载

一、精心选一选

1. a的倒数是3，则a的值是（）

A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 位于环水东湾新城区的茂名市第一中学新校区占地面积约为536.5亩．将536.5用科学记数法可表示为（）

A、0.5365×10³ B、5.365×10² C、53.65×10 D、536.5

查看试题解析
3. 如图，AB是⊙O的直径，AB⊥CD于点E，若CD=6，则DE=（）

A、3 B、4 C、5 D、6

查看试题解析
4. 方程组 ${\begin{matrix} x - y = 1 \\ x + y = 5 \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = 1 \\ y = 4 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ C、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$ D、 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$

查看试题解析
5.
一个正方体的表面展开图如图所示，则原正方体的“建”字所在的面的对面所标的字是（）

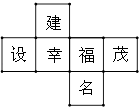A、设 B、福 C、茂 D、名

查看试题解析
6. 从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是（）

A、6 B、7 C、8 D、9

查看试题解析
7. 下列调查中，适宜采用全面调查（普查）方式的是（）

A、对一批圆珠笔使用寿命的调查 B、对全国九年级学生身高现状的调查 C、对某品牌烟花爆竹燃放安全的调查 D、对一枚用于发射卫星的运载火箭各零部件的检查

查看试题解析
8. 某中学初三（1）班的一次数学测试的平均成绩为80分，男生平均成绩为82分，女生平均成绩为77分，则该班男、女生的人数之比为（）

A、1：2 B、2：1 C、3：2 D、2：3

查看试题解析
9. 如果x＜0，y＞0，x+y＜0，那么下列关系式中正确的是（）

A、x＞y＞﹣y＞﹣x B、﹣x＞y＞﹣y＞x C、y＞﹣x＞﹣y＞x D、﹣x＞y＞x＞﹣y

查看试题解析
10. 如图，四边形ABCD四边的中点分别为E，F，G，H，对角线AC与BD相交于点O，若四边形EFGH的面积是3，则四边形ABCD的面积是（）

A、3 B、6 C、9 D、12

查看试题解析

二、细心填一填

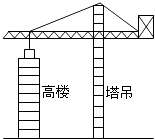
11. 分解因式：x²y﹣y= ．

查看试题解析
12. 如图所示，建高楼常需要用塔吊来吊建筑材料，而塔吊的上部是三角形结构，这是应用了三角形的哪个性质？答：．（填“稳定性”或“不稳定性”）

查看试题解析
13. 若分式 $\frac{a^{2} - 9}{a + 3}$ 的值为0，则a的值是．

查看试题解析
14. 如图，在3×3的方格中（共有9个小格），每个小方格都是边长为1的正方形，O、B、C是格点，则扇形OBC的面积等于（结果保留π）

查看试题解析
15. 如图，⊙O与直线l₁相离，圆心O到直线l₁的距离OB=2 $\sqrt{3}$ ，OA=4，将直线l₁绕点A逆时针旋转30°后得到的直线l₂刚好与⊙O相切于点C，则OC= ．

查看试题解析

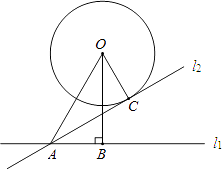
三、用心做一做

16. 先化简，后求值：a（a+1）﹣（a+1）（a﹣1），其中a=3．

查看试题解析
17. 求不等式组 ${\begin{matrix} x + 2 > 1 \\ 3 x - 5 \leq 0 \end{matrix}$ 的整数解．

查看试题解析
18. 如图，在直角坐标系中，线段AB的两个端点的坐标分别为A（﹣3，0），B（0，4）．

(1)、画出线段AB先向右平移3个单位，再向下平移4个单位后得到的线段CD，并写出A的对应点D的坐标，B的对应点C的坐标；

(2)、连接AD、BC，判断所得图形的形状．（直接回答，不必证明）

查看试题解析

四、沉着冷静，缜密思考

19. 某校计划组织学生到市影剧院观看大型感恩歌舞剧，为了解学生如何去影剧院的问题，学校随机抽取部分学生进行调查，并将调查结果制成了表格、条形统计图和扇形统计图（均不完整）．

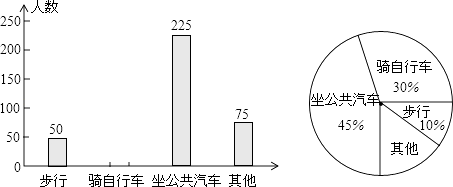(1)、此次共调查了多少位学生？

(2)、将表格填充完整；
步行
骑自行车
坐公共汽车
其他
50

(3)、将条形统计图补充完整．

查看试题解析
20. 在4张完全相同的卡片正面分别写上数字1，2，3，3，现将它们的背面朝上洗均匀．

(1)、随机抽出一张卡片，求抽到数字“3”的概率；

(2)、若随机抽出一张卡片记下数字后放回并洗均匀，再随机抽出一张卡片，求两次都是抽到数字“3”的概率；（要求画树状图或列表求解）

(3)、如果再增加若干张写有数字“3”的同样卡片，洗均匀后，使得随机抽出一张卡片是数字“3”的概率为 $\frac{3}{4}$ ，问增加了多少张卡片？

查看试题解析

五、满怀信心，再接再厉

21. 如图，已知矩形ABCD中，F是BC上一点，且AF=BC，DE⊥AF，垂足是E，连接DF．求证：

(1)、△ABF≌△DEA；

(2)、DF是∠EDC的平分线．

查看试题解析
22. 每年六七月份我市荔枝大量上市，今年某水果商以5元/千克的价格购进一批荔枝进行销售，运输过程中质量损耗5%，运输费用是0.7元/千克，假设不计其他费用．

(1)、水果商要把荔枝售价至少定为多少才不会亏本？

(2)、在销售过程中，水果商发现每天荔枝的销售量m（千克）与销售单价x（元/千克）之间满足关系：m=﹣10x+120，那么当销售单价定为多少时，每天获得的利润w最大？

查看试题解析
23. 如图，以AB为直径的⊙O是△ADC的外接圆，过点O作PO⊥AB，交AC于点E，PC的延长线交AB的延长线于点F，∠PEC=∠PCE．

(1)、求证：FC为⊙O的切线；

(2)、若△ADC是边长为a的等边三角形，求AB的长．（用含a的代数式表示）

查看试题解析

六、灵动智慧，超越自我

24. 阅读下面材料，然后解答问题：
在平面直角坐标系中，以任意两点P（x₁ ， y₁），Q（x₂ ， y₂）为端点的线段的中点坐标为（ $\frac{x_{1} + x_{2}}{2}$ ， $\frac{y_{1} + y_{2}}{2}$ ）．如图，在平面直角坐标系xOy中，双曲线y= $\frac{- 3}{x}$ （x＜0）和y= $\frac{k}{x}$ （x＞0）的图象关于y轴对称，直线y= $\frac{1}{2} x$ + $\frac{5}{2}$ 与两个图象分别交于A（a，1），B（1，b）两点，点C为线段AB的中点，连接OC、OB．

(1)、求a、b、k的值及点C的坐标；

(2)、若在坐标平面上有一点D，使得以O、C、B、D为顶点的四边形是平行四边形，请求出点D的坐标．

查看试题解析
25.
如图所示，抛物线y=ax²+ $\frac{3}{2} x$ +c经过原点O和A（4，2），与x轴交于点C，点M、N同时从原点O出发，点M以2个单位/秒的速度沿y轴正方向运动，点N以1个单位/秒的速度沿x轴正方向运动，当其中一个点停止运动时，另一点也随之停止．

(1)、求抛物线的解析式和点C的坐标；

(2)、在点M、N运动过程中，
①若线段MN与OA交于点G，试判断MN与OA的位置关系，并说明理由；
②若线段MN与抛物线相交于点P，探索：是否存在某一时刻t，使得以O、P、A、C为顶点的四边形是等腰梯形？若存在，请求出t值；若不存在，请说明理由．

查看试题解析

步行	骑自行车	坐公共汽车	其他
50