吉林省长春市汽开区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-03-12 类型:期末考试
一、选择题
-
1. 若关于x的方程(m﹣1)x2+mx﹣1=0是一元二次方程,则m的取值范围是( )A、m≠1 B、m=1 C、m≥1 D、m≠02. 抛物线y=x2+x﹣1的对称轴是( )A、直线x=﹣1 B、直线x=1 C、直线x=﹣
 D、直线x=
D、直线x=  3. 将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )A、y=(x+1)2+4 B、y=(x+1)2+2 C、y=(x﹣1)2+4 D、y=(x﹣1)2+24. 如图,在△ABC中,D、E分别是AB、AC的中点,若△ADE的面积是a,则四边形BDEC的面积是( )
3. 将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )A、y=(x+1)2+4 B、y=(x+1)2+2 C、y=(x﹣1)2+4 D、y=(x﹣1)2+24. 如图,在△ABC中,D、E分别是AB、AC的中点,若△ADE的面积是a,则四边形BDEC的面积是( )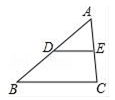 A、a B、2a C、3a D、4a5. 如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A、a B、2a C、3a D、4a5. 如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( ) A、
A、 B、
B、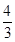 C、
C、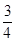 D、
D、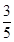 6. 如图,AB为⊙O直径,已知圆周角∠BCD=30°,则∠ABD为( )
6. 如图,AB为⊙O直径,已知圆周角∠BCD=30°,则∠ABD为( )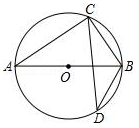 A、30° B、40° C、50° D、60°7. 如图,⊙O的直径AB=6,若∠BAC=50°,则劣弧AC的长为( )
A、30° B、40° C、50° D、60°7. 如图,⊙O的直径AB=6,若∠BAC=50°,则劣弧AC的长为( ) A、2π B、
A、2π B、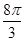 C、
D、
C、
D、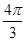 8. 二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,则方程ax2+bx+c=m有实数根的条件是( )
8. 二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,则方程ax2+bx+c=m有实数根的条件是( ) A、m≥﹣4 B、m≥0 C、m≥5 D、m≥6
A、m≥﹣4 B、m≥0 C、m≥5 D、m≥6二、填空题
-
9. 已知x=2是一元二次方程x2+mx+2=0的一个解,则m的值是 .10. 某校对初三(2)班40名学生体育考试中“立定跳远”项目的得分情况进行了统计,结果如下表,
得分
10分
9分
8分
7分
6分以下
人数(人)
20
12
5
2
1
根据表中数据,若随机抽取该班的一名学生,则该学生“立定跳远”得分恰好是10分的概率是 .
11. 函数y=x2﹣2x﹣4的最小值为 .12. 我国南宋数学家杨辉在1275年提出了一个问题:直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步).问阔及长各几步?若设阔(宽)为x步,则所列方程为 .13. 如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= .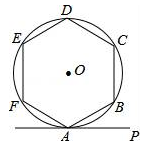 14. 如图,抛物线y=﹣2x2+2与x轴交于点A、B,其顶点为E.把这条抛物线在x轴及其上方的部分记为C1 , 将C1向右平移得到C2 , C2与x轴交于点B、D,C2的顶点为F,连结EF.则图中阴影部分图形的面积为 .
14. 如图,抛物线y=﹣2x2+2与x轴交于点A、B,其顶点为E.把这条抛物线在x轴及其上方的部分记为C1 , 将C1向右平移得到C2 , C2与x轴交于点B、D,C2的顶点为F,连结EF.则图中阴影部分图形的面积为 .
三、解答题
-
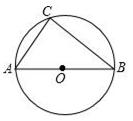
15. 解方程:x2+4x﹣7=0.16. 如图,AB是⊙O的直径,⊙O的半径为5cm,弦AC的长为6cm,求弦BC的长.
 17. 如图是一副扑克牌中的三张牌,将它们正面向下洗均匀,甲同学从中随机抽取一张牌后放回,乙同学再从中随机抽取一张牌,用树状图(或列表)的方法,求抽出的两张牌中,牌面上的数字都是偶数的概率.
17. 如图是一副扑克牌中的三张牌,将它们正面向下洗均匀,甲同学从中随机抽取一张牌后放回,乙同学再从中随机抽取一张牌,用树状图(或列表)的方法,求抽出的两张牌中,牌面上的数字都是偶数的概率. 18. 如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,以点C为圆心,以2cm长为半径作圆,试判断⊙C与AB的位置关系.
18. 如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,以点C为圆心,以2cm长为半径作圆,试判断⊙C与AB的位置关系. 19. 如图,为了测量旗杆的高度BC,在距旗杆底部B点10米的A处,用高1.5米的测角仪DA测得旗杆顶端C的仰角∠CDE为52°,求旗杆BC的高度.(结果精确到0.1米)【参考数据sin52°=0.79,cos52°=0.62,tan52°=1.28】
19. 如图,为了测量旗杆的高度BC,在距旗杆底部B点10米的A处,用高1.5米的测角仪DA测得旗杆顶端C的仰角∠CDE为52°,求旗杆BC的高度.(结果精确到0.1米)【参考数据sin52°=0.79,cos52°=0.62,tan52°=1.28】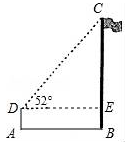 20. 在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
20. 在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).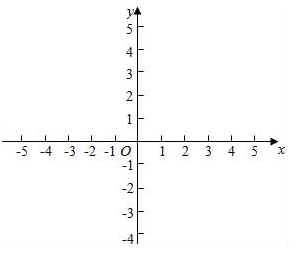 (1)、求这条抛物线所对应的二次函数的表达式.(2)、直接写出该抛物线开口方向和顶点坐标.(3)、直接在所给坐标平面内画出这条抛物线.21. 如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)、求这条抛物线所对应的二次函数的表达式.(2)、直接写出该抛物线开口方向和顶点坐标.(3)、直接在所给坐标平面内画出这条抛物线.21. 如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°. (1)、求证:BD是⊙O的切线.(2)、若OA=8,求OA、OD与 围成的扇形的面积.22. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)、求证:BD是⊙O的切线.(2)、若OA=8,求OA、OD与 围成的扇形的面积.22. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.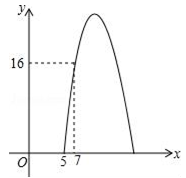 (1)、m= , n= .(2)、销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?(3)、该种商品每天的销售利润不低于16元时,直接写出x的取值范围.23. 如图
(1)、m= , n= .(2)、销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?(3)、该种商品每天的销售利润不低于16元时,直接写出x的取值范围.23. 如图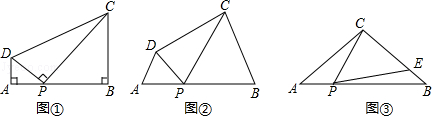
【感知】如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
【探究】如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)、求证:△DAP~△PBC.(2)、若PD=5,PC=10,BC=9,求AP的长.【应用】如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
24. 如图,在平面直角坐标系中,直线y=﹣x+3与抛物线y=﹣x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣1.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q,当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.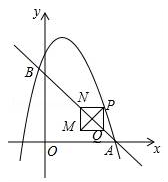 (1)、求b、c的值.(2)、当点N落在直线AB上时,直接写出m的取值范围.(3)、当点P在A、B两点之间的抛物线上运动时,设正方形PQMN周长为c,求c与m之间的函数关系式,并写出c随m增大而增大时m的取值范围.(4)、当△PQM与y轴只有1个公共点时,直接写出m的值.
(1)、求b、c的值.(2)、当点N落在直线AB上时,直接写出m的取值范围.(3)、当点P在A、B两点之间的抛物线上运动时,设正方形PQMN周长为c,求c与m之间的函数关系式,并写出c随m增大而增大时m的取值范围.(4)、当△PQM与y轴只有1个公共点时,直接写出m的值.