广东省东莞市2018-2019学年高三上学期理数期末调研测试试卷
试卷更新日期:2019-03-12 类型:期末考试
一、单选题
-
1. 设集合 , ,则 ( )A、
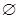 B、
B、 C、
C、 D、
D、 2. 已知复数 满足 ( 为虚数单位),则 ( )A、2 B、 C、
2. 已知复数 满足 ( 为虚数单位),则 ( )A、2 B、 C、 D、
D、 3. 假设东莞市市民使用移动支付的概率都为 ,且每位市民使用支付方式都相互独立的,已知 是其中10位市民使用移动支付的人数,且 ,则 的值为( )A、0.4 B、0.5 C、0.6 D、0.84. 已知向量 , ,若 ,则实数 的值为( )A、-2 B、0 C、1 D、25. 函数 的图像大致为 ( )A、
3. 假设东莞市市民使用移动支付的概率都为 ,且每位市民使用支付方式都相互独立的,已知 是其中10位市民使用移动支付的人数,且 ,则 的值为( )A、0.4 B、0.5 C、0.6 D、0.84. 已知向量 , ,若 ,则实数 的值为( )A、-2 B、0 C、1 D、25. 函数 的图像大致为 ( )A、 B、
B、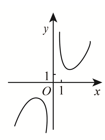 C、
C、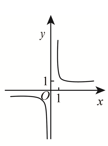 D、
D、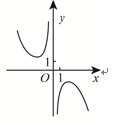 6. 已知某几何体的三视图如图所示(侧视图中曲线为四分之一圆弧),则该几何体的体积为( )
6. 已知某几何体的三视图如图所示(侧视图中曲线为四分之一圆弧),则该几何体的体积为( ) A、
A、 B、
B、 C、
C、 D、4
7. 二项式 的展开式的常数项为( )A、
D、4
7. 二项式 的展开式的常数项为( )A、 B、15
C、
B、15
C、 D、
D、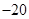 8. 在各项均为正数的等比数列 中,若 ,则 ( )A、6 B、7 C、8 D、99. 过点 且倾斜角为 的直线 交圆 于 , 两点,则弦 的长为( )A、
8. 在各项均为正数的等比数列 中,若 ,则 ( )A、6 B、7 C、8 D、99. 过点 且倾斜角为 的直线 交圆 于 , 两点,则弦 的长为( )A、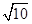 B、
B、 C、
D、
C、
D、 10. 已知直线 与曲线 相切,则 ( )A、
10. 已知直线 与曲线 相切,则 ( )A、 B、
B、 C、
C、 D、
D、 11. 已知奇函数 的导函数为 ,且 ,当 时 恒成立,则使得 成立的 的取值范围为( )A、
11. 已知奇函数 的导函数为 ,且 ,当 时 恒成立,则使得 成立的 的取值范围为( )A、 B、
B、 C、
C、 D、
D、 12. 圆锥 (其中 为顶点, 为底面圆心)的侧面积与底面积的比是 ,则圆锥 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )A、
12. 圆锥 (其中 为顶点, 为底面圆心)的侧面积与底面积的比是 ,则圆锥 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 设随机变量 ,且 ,则 .14. 在 中,角 , , 所对的边分别为 , , ,已知 , , 的面积为 ,则边 .15. 实数 , 满足 ,且 ,则 的最小值为 .16. 已知函数 ,则 的最小值为 .
三、解答题
-
17. 已知等差数列 的前 项和为 ,且 , .(1)、求数列 的通项公式;(2)、求 的值.18. 如图,在 中,角 , , 所对的边分别为 , , ,且 .
 (1)、求角 的大小;(2)、若 边上的中线 的长为 ,且 ,求 的长.19. 如图所示,在四棱锥 中,底面 为菱形, 底面 ,点 是 上的一个动点, , .
(1)、求角 的大小;(2)、若 边上的中线 的长为 ,且 ,求 的长.19. 如图所示,在四棱锥 中,底面 为菱形, 底面 ,点 是 上的一个动点, , . (1)、当 时,求证: ;(2)、当 平面 时,求二面角 的余弦值.20. 如表提供了工厂技术改造后某种型号设备的使用年限 和所支出的维修费 (万元)的几组对照数据:
(1)、当 时,求证: ;(2)、当 平面 时,求二面角 的余弦值.20. 如表提供了工厂技术改造后某种型号设备的使用年限 和所支出的维修费 (万元)的几组对照数据:(年)
2
3
4
5
6
(万元)
1
2.5
3
4
4.5
参考公式: , .
(1)、若知道 对 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出 关于 的线性回归方程 ;(2)、已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?