广东省2018-2019学年高三上学期理数期末质量检测试卷
试卷更新日期:2019-03-12 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 复数 在复平面内对应的点的坐标为( )A、
2. 复数 在复平面内对应的点的坐标为( )A、 B、
B、 C、
C、 D、
D、 3. 若 ,且 为第四象限角,则 的值等于( )A、
3. 若 ,且 为第四象限角,则 的值等于( )A、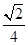 B、
B、 C、
D、
C、
D、 4. 已知左、右焦点分别为 的双曲线 : 过点 ,点 在双曲线 上,若 ,则 ( )A、 B、 C、
4. 已知左、右焦点分别为 的双曲线 : 过点 ,点 在双曲线 上,若 ,则 ( )A、 B、 C、 D、
5. 已知 ,下列函数中,在其定义域内是单调递增函数且图象关于原点对称的是( )A、
D、
5. 已知 ,下列函数中,在其定义域内是单调递增函数且图象关于原点对称的是( )A、 B、
B、 C、
C、 D、
D、 6. 若干年前,某教师刚退休的月退休金为 元,月退休金各种用途占比统计图如下面的条形图。该教师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图。已知目前的月就医费比刚退休时少 元,则目前该教师的月退休金为( )
6. 若干年前,某教师刚退休的月退休金为 元,月退休金各种用途占比统计图如下面的条形图。该教师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图。已知目前的月就医费比刚退休时少 元,则目前该教师的月退休金为( )
 A、
A、 元
B、
元
B、 元
C、
元
C、 元
D、
元
D、 元
7. 已知向量 与 共线且方向相同,则 ( )A、
元
7. 已知向量 与 共线且方向相同,则 ( )A、 B、
B、 C、
C、 D、
D、 8. 拿破仑为人好学,是法兰西科学院院士,他对数学方面很感兴趣,在行军打仗的空闲时间,经常研究平面几何。他提出了著名的拿破仑定理:以三角形各边为边分别向外(内)侧作等边三角形,则它们的中心构成一个等边三角形。如图所示,以等边 的三条边为边,向外作 个正三角形,取它们的中心 ,顺次连接,得到 ,图中阴影部分为 与 的公共部分。若往 中投掷一点,则该点落在阴影部分内的概率为( )
8. 拿破仑为人好学,是法兰西科学院院士,他对数学方面很感兴趣,在行军打仗的空闲时间,经常研究平面几何。他提出了著名的拿破仑定理:以三角形各边为边分别向外(内)侧作等边三角形,则它们的中心构成一个等边三角形。如图所示,以等边 的三条边为边,向外作 个正三角形,取它们的中心 ,顺次连接,得到 ,图中阴影部分为 与 的公共部分。若往 中投掷一点,则该点落在阴影部分内的概率为( ) A、 B、 C、 D、9. 已知函数 的最大值为 ,周期为 ,将函数 的图象向左平移 个单位长度得到 的图象,若 是偶函数,则 的解析式为( )A、
A、 B、 C、 D、9. 已知函数 的最大值为 ,周期为 ,将函数 的图象向左平移 个单位长度得到 的图象,若 是偶函数,则 的解析式为( )A、 B、
B、 C、
C、 D、
D、 10. 如图所示为某三棱锥的三视图,则该三棱锥外接球的表面积为( )
10. 如图所示为某三棱锥的三视图,则该三棱锥外接球的表面积为( ) A、
A、 B、
B、 C、
C、 D、
D、 11. 在凸平面四边形 中, ,且 , , ,则 的面积 等于( )A、
11. 在凸平面四边形 中, ,且 , , ,则 的面积 等于( )A、 B、
B、 C、
C、 D、
D、 12. 已知函数 在 上存在导函数 ,若 ,且 时 ,则不等式 的解集为( )A、
12. 已知函数 在 上存在导函数 ,若 ,且 时 ,则不等式 的解集为( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 二项式 展开式中的常数项为。(用数字作答)14. 已知实数 满足 ,则 的最小值为。15. 已知正方体 的棱长为 , 交 于 , 是棱 的中点,则直线 被正方体外接球所截得的线段长度为。
 16. 已知抛物线 : 经过点 ,直线 分别与抛物线 交于点 ,若直线 的斜率之和为零,则直线 的斜率为。
16. 已知抛物线 : 经过点 ,直线 分别与抛物线 交于点 ,若直线 的斜率之和为零,则直线 的斜率为。三、解答题
-
17. 已知数列 是递增的等差数列, ,且 是 与 的等比中项。(1)、求 ;(2)、若 ,求数列 的前 项和 。18. 水果的价格会受到需求量和天气的影响.某采购员定期向某批发商购进某种水果,每箱水果的价格会在当日市场价的基础上进行优惠,购买量越大优惠幅度越大,采购员通过对以往的10组数据进行研究,发现可采用 来作为价格的优惠部分 (单位:元/箱)与购买量 (单位:箱)之间的回归方程,整理相关数据得到下表(表中 ):
 (1)、根据参考数据,
(1)、根据参考数据,①建立 关于 的回归方程;
②若当日该种水果的市场价为200元/箱,估算购买100箱该种水果所需的金额(精确到0.1元).
(2)、在样本中任取一点,若它在回归曲线上或上方,则称该点为高效点.已知这10个样本点中,高效点有4个,现从这10个点中任取3个点,设取到高效点的个数为 ,求 的数学期望.附:对于一组数据 , ,…, ,其回归直线 的斜率和截距的最小二乘估计分别为 , ,参考数据:
19. 在多面体 中, 是边长为 的正方形, ,平面 平面 , , 。 (1)、求证: 平面 ;(2)、求直线 与平面 所成角的正弦值。20. 已知椭圆 : 的左、右焦点分别为 , 是椭圆 上的点,且 的面积为 。(1)、求椭圆 的方程;(2)、若斜率为 且在 轴上的截距为 的直线 与椭圆 相交于两点 ,若椭圆 上存在点 ,满足 ,其中 是坐标原点,求 的值。
(1)、求证: 平面 ;(2)、求直线 与平面 所成角的正弦值。20. 已知椭圆 : 的左、右焦点分别为 , 是椭圆 上的点,且 的面积为 。(1)、求椭圆 的方程;(2)、若斜率为 且在 轴上的截距为 的直线 与椭圆 相交于两点 ,若椭圆 上存在点 ,满足 ,其中 是坐标原点,求 的值。