2018-2019学年初中数学北师大版七年级下册4.3 探索三角形全等的条件 同步练习
试卷更新日期:2019-03-12 类型:同步测试
一、单选题
-
1. 如图,工人师傅物门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
 A、两点之间的线段最短 B、三角形有稳定性 C、长方形的四个角都是直角 D、长方形是轴对称图形2. 如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A、两点之间的线段最短 B、三角形有稳定性 C、长方形的四个角都是直角 D、长方形是轴对称图形2. 如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )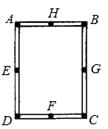 A、E,G之间 B、A,C之间 C、G,H之间 D、B,F之间3. 如图,已知 AD∥BC,AB=CD,AC,BD 交于点 O,另加一个 条件不能使△ABD≌△CDB 的是( )
A、E,G之间 B、A,C之间 C、G,H之间 D、B,F之间3. 如图,已知 AD∥BC,AB=CD,AC,BD 交于点 O,另加一个 条件不能使△ABD≌△CDB 的是( ) A、AO=CO B、AD=BC C、AC=BD D、OB=OD4. 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如右图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A、AO=CO B、AD=BC C、AC=BD D、OB=OD4. 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如右图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( ) A、边角边 B、角边角 C、边边边 D、边边角5. 如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )
A、边角边 B、角边角 C、边边边 D、边边角5. 如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )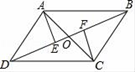 A、5对 B、6对 C、7对 D、8对6. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( ).
A、5对 B、6对 C、7对 D、8对6. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( ). A、SAS B、AAS C、ASA D、 SSS7. 以下说法正确的是( )
A、SAS B、AAS C、ASA D、 SSS7. 以下说法正确的是( )①一条直角边和斜边上的高对应相等的两个直角三角形全等;②有两条边相等的两个直角三角形全等;③有一边相等的两个等边三角形全等;④两边和其中一边的对角对应相等的两个三角形全等.
A、①② B、②④ C、①③ D、①③④8. 如图,是玩具拼图模板的一部分,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中能和△ABC完全重合的是( ) A、甲和丙 B、丙和乙 C、只有甲 D、只有丙9. 下列条件中,不能判定△ABC≌△A′B′C′,的是( )A、∠A=∠A,∠C=∠C,AC=A′C′ B、∠B=∠B′,BC=B′C′,AB=A′B′ C、∠A=∠A′=80°,∠B=60°,∠C′=40°,AB=A′B′ D、∠A=∠A′,BC=B′C′,AB=A′B′10. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )A、
A、甲和丙 B、丙和乙 C、只有甲 D、只有丙9. 下列条件中,不能判定△ABC≌△A′B′C′,的是( )A、∠A=∠A,∠C=∠C,AC=A′C′ B、∠B=∠B′,BC=B′C′,AB=A′B′ C、∠A=∠A′=80°,∠B=60°,∠C′=40°,AB=A′B′ D、∠A=∠A′,BC=B′C′,AB=A′B′10. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )A、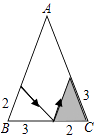 B、
B、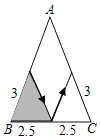 C、
C、 D、
D、
二、填空题
-
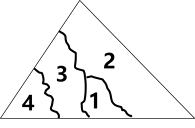
11. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的带去,就能配一块大小和形状与原来都一样的三角形。
 12. 如图,在四边形ABCD中,AB=CB,AD=CD.若∠A=108°,则∠C的大小=(度).
12. 如图,在四边形ABCD中,AB=CB,AD=CD.若∠A=108°,则∠C的大小=(度).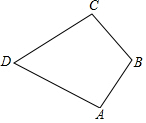 13. 如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是 .
13. 如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是 . 14. 如图,已知∠ACB=∠DBC,请添加一个条件 , 使得△ABC≌△DCB.
14. 如图,已知∠ACB=∠DBC,请添加一个条件 , 使得△ABC≌△DCB. 15. 已知△ABC中,AB=6cm,AC=8cm,AD为边BC上的中线,则中线AD的取值范围是16. 如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动分钟后△CAP与△PQB全等.
15. 已知△ABC中,AB=6cm,AC=8cm,AD为边BC上的中线,则中线AD的取值范围是16. 如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动分钟后△CAP与△PQB全等.
三、解答题
-
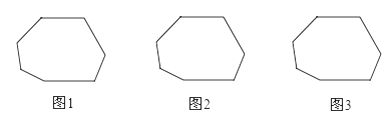
17. 小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理.
 18. 数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:作法:如图1,①在OA和OB上分别截取OD、OE,使OD=OE.②分别以D、E为圆心,以大于12DE的长为半径作弧,两弧在∠AOB内交于点C.③作射线OC,则OC就是∠AOB的平分线.小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
18. 数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:作法:如图1,①在OA和OB上分别截取OD、OE,使OD=OE.②分别以D、E为圆心,以大于12DE的长为半径作弧,两弧在∠AOB内交于点C.③作射线OC,则OC就是∠AOB的平分线.小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.①李老师用尺规作角平分线时,用到的三角形全等的判定方法是.
②请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
 19. 如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P
19. 如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P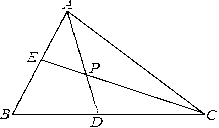 (1)、求∠CPD的度数(2)、若AE=3,CD=7,求线段AC的长.20. 如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD.
(1)、求∠CPD的度数(2)、若AE=3,CD=7,求线段AC的长.20. 如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD.
求证:
(1)、△ABC≌△DCB.(2)、∠ABO=∠DCO21. 如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。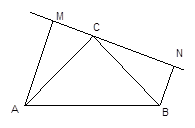
 (1)、求证:MN=AM+BN;(2)、若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。22. 如图
(1)、求证:MN=AM+BN;(2)、若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。22. 如图 (1)、如图①,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;(2)、如图②,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)、如图③,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.23. 如图1,在Rt△ACB中,∠BAC=90°,AB=AC,分别过B、C两点作过点A的直线l的垂线,垂足为D、E;
(1)、如图①,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;(2)、如图②,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)、如图③,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.23. 如图1,在Rt△ACB中,∠BAC=90°,AB=AC,分别过B、C两点作过点A的直线l的垂线,垂足为D、E; (1)、如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、如图3,∠BAC=90°,AB=16,AC=20.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,各自到达终点时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?(直接写出答案)
(1)、如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、如图3,∠BAC=90°,AB=16,AC=20.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,各自到达终点时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?(直接写出答案)