2018-2019学年初中数学北师大版七年级下册3.3用图象表示的变量间关系 同步练习
试卷更新日期:2019-03-12 类型:同步测试
一、单选题
-
1. 在用图象表示变量之间的关系时,下列说法最恰当的是( )A、用水平方向的数轴上的点表示相应的函数值 B、用竖直方向的数轴上的点表示自变量 C、用横轴上的点表示自变量 D、用横轴或纵轴上的点表示自变量2. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
 A、
A、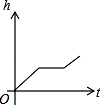 B、
B、 C、
C、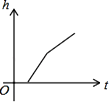 D、
D、 3. 如图,是某蓄水池的横断面示意图,蓄水池分为深水区和浅水区,如果向这个蓄水池以固定的速度注水,下面能表示水的深度h与时间t的关系的图象大致是( )
3. 如图,是某蓄水池的横断面示意图,蓄水池分为深水区和浅水区,如果向这个蓄水池以固定的速度注水,下面能表示水的深度h与时间t的关系的图象大致是( )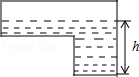 A、
A、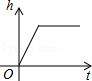 B、
B、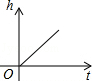 C、
C、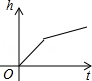 D、
D、 4. 在物理实验课上,老师用弹簧秤将铁块悬于盛有水的水槽中,然后匀速向上提起,直到铁块完全露出水面一定高度,则下图能反映弹簧秤的读数 (单位 )与铁块被提起的高度 (单位 )之间的函数关系的大致图象是( )
4. 在物理实验课上,老师用弹簧秤将铁块悬于盛有水的水槽中,然后匀速向上提起,直到铁块完全露出水面一定高度,则下图能反映弹簧秤的读数 (单位 )与铁块被提起的高度 (单位 )之间的函数关系的大致图象是( )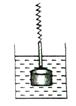 A、
A、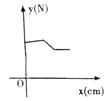 B、
B、 C、
C、 D、
D、 5. 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )A、
5. 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )A、 B、
B、 C、
C、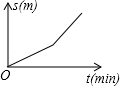 D、
D、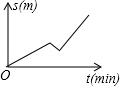 6. 均匀地向一个容器注水,最后将容器注满 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是
6. 均匀地向一个容器注水,最后将容器注满 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是 A、
A、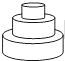 B、
B、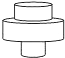 C、
C、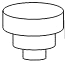 D、
D、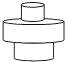 7. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则此函数( )
7. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则此函数( )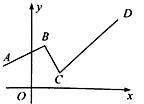 A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小8. 如图,下列各情境的描述中,与图象大致吻合的是( )
A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小8. 如图,下列各情境的描述中,与图象大致吻合的是( ) A、一足球被用力踢出去(高度与时间的关系) B、一辆汽车在匀速行驶(速度与时间的关系) C、一面旗子在冉冉升起(高度与时间的关系) D、一杯开水正在晾凉(温度与时间的关系)9. 下列四个函数图象中,当x<0时,y随x的增大而减小的是( )A、
A、一足球被用力踢出去(高度与时间的关系) B、一辆汽车在匀速行驶(速度与时间的关系) C、一面旗子在冉冉升起(高度与时间的关系) D、一杯开水正在晾凉(温度与时间的关系)9. 下列四个函数图象中,当x<0时,y随x的增大而减小的是( )A、 B、
B、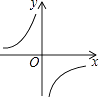 C、
C、 D、
D、 10. 如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
10. 如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( ) A、点C B、点O C、点E D、点F
A、点C B、点O C、点E D、点F二、填空题
-
11. 小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是(只需填号).
 12. 已知甲、乙两车分别从A、B两地同时出发,以各自的速度匀速相向而行,两车相遇后,乙车继续向终点A地行使,而甲车原地停留了一段时间后才继续驶向终点B地,两车到达各自的终点后分别停止运动.若整个过程中,甲、乙两车各自的速度均保持不变,且甲、乙两车之间的距离s(千米)与乙车行驶时间t(小时)的函数图象如图所示,则甲车比乙车早到小时.
12. 已知甲、乙两车分别从A、B两地同时出发,以各自的速度匀速相向而行,两车相遇后,乙车继续向终点A地行使,而甲车原地停留了一段时间后才继续驶向终点B地,两车到达各自的终点后分别停止运动.若整个过程中,甲、乙两车各自的速度均保持不变,且甲、乙两车之间的距离s(千米)与乙车行驶时间t(小时)的函数图象如图所示,则甲车比乙车早到小时.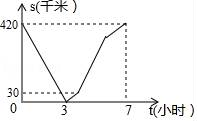 13.
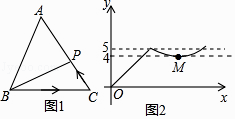
13.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .
 14. 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示,当总用水量为2500米3时,该经济作物种植时间是天.
14. 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示,当总用水量为2500米3时,该经济作物种植时间是天. 15. 如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
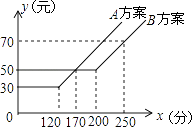
15. 如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:①若通话时间少于120分,则A方案比B方案便宜20元;
②若通话时间超过200分,则B方案比A方案便宜12元;
③若通讯费用为60元,则B方案比A方案的通话时间多;
④若两种方案通讯费用相差10元,则通话时间是145分或185分.其中正确结论的序号是 .
 16. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
16. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 . (把你认为正确说法的序号都填上)

三、解答题
-
17. 如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
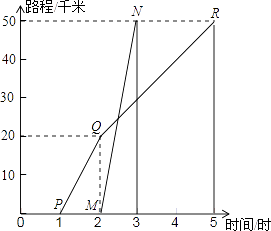 (1)、甲和乙哪一个出发的更早?早出发多长时间?(2)、甲和乙哪一个早到达B城?早多长时间?(3)、乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?(4)、请你根据图象上的数据,求出乙出发用多长时间就追上甲?18.
(1)、甲和乙哪一个出发的更早?早出发多长时间?(2)、甲和乙哪一个早到达B城?早多长时间?(3)、乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?(4)、请你根据图象上的数据,求出乙出发用多长时间就追上甲?18.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
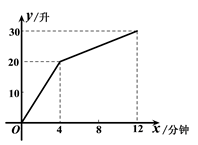 19.
19.如图是某地某天温度变化的情况,根据图象回答问题:
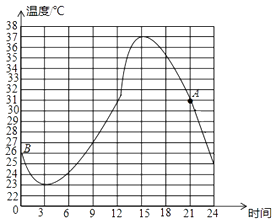 (1)、上午3时的气温是多少?(2)、这一天的最高温度和最低温度分别是多少?(3)、这一天的温差是多少?从最低温度到最高温经过了多长时间?(4)、图中A点表示的是什么?B点呢?
(1)、上午3时的气温是多少?(2)、这一天的最高温度和最低温度分别是多少?(3)、这一天的温差是多少?从最低温度到最高温经过了多长时间?(4)、图中A点表示的是什么?B点呢?
20.如图表示的是汽车在行驶的过程中,速度随时间变化而变化的情况.
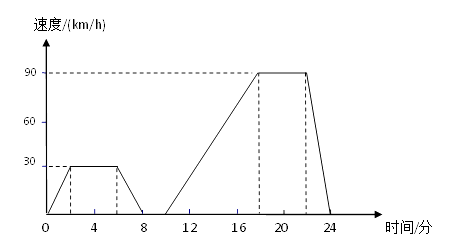 (1)、汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?(2)、汽车在那些时间段保持匀速行驶?时速分别是多少?(3)、出发后8分到10分之间可能发生了什么情况?(4)、用自己的语言大致描述这辆汽车的行驶情况.21.
(1)、汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?(2)、汽车在那些时间段保持匀速行驶?时速分别是多少?(3)、出发后8分到10分之间可能发生了什么情况?(4)、用自己的语言大致描述这辆汽车的行驶情况.21.人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的东西会逐渐遗忘.为提升记忆的效果,需要有计划的按时复习巩固.图中的实线部分是记忆保持量(%)与时间(天)之间的关系图.请根据图回答下列问题:
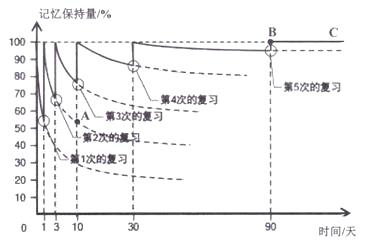 (1)、图中的自变量是 , 因变量是;(2)、如果不复习,3天后记忆保持量约为;(3)、图中点A表示的意义是;(4)、图中射线BC表示的意义是;(5)、经过第1次复习与不进行复习,3天后记忆保持量相差约为;(6)、10天后,经过第2次复习与从来都没有复习的记忆保持量相差约为.22.
(1)、图中的自变量是 , 因变量是;(2)、如果不复习,3天后记忆保持量约为;(3)、图中点A表示的意义是;(4)、图中射线BC表示的意义是;(5)、经过第1次复习与不进行复习,3天后记忆保持量相差约为;(6)、10天后,经过第2次复习与从来都没有复习的记忆保持量相差约为.22.暑假就要来了,小明为自己制定了慢跑锻炼计划,某日小明从家出发沿解放路慢跑,已知他离家的距离s(千米)与时间t(分钟)之间的关系如图所示,请根据图象直接回答下列问题:
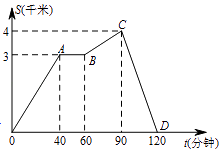 (1)、小明离开家的最远距离是多少千米,他在120分钟内共跑了多少千米;(2)、小明在这次慢跑过程中,停留所用的时间为多少分钟;(3)、小明在这段时间内慢跑的最快速度是每小时多少千米.
(1)、小明离开家的最远距离是多少千米,他在120分钟内共跑了多少千米;(2)、小明在这次慢跑过程中,停留所用的时间为多少分钟;(3)、小明在这段时间内慢跑的最快速度是每小时多少千米.