2015年浙江省舟山市中考数学试卷

试卷更新日期：2017-04-24 类型：中考真卷

进入出卷网下载

一、选择题

1. 计算2﹣3的结果为（）

A、﹣1 B、﹣2 C、1 D、2

查看试题解析
2.
下列四个图形分别是四届国际数学家大会的会标，其中属于中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 截至今年4月10日，舟山全市需水量为84 327 000m³ ，数据84 327 000用科学记数法表示为（　　）

A、0.84327×10⁸ B、8.4327×10⁷ C、8.4327×10⁸ D、84327×10³

查看试题解析
4. 质检部门为了检测某品牌电器的质量，从同一批次共10000件产品中随机抽取100件进行检测，检测出次品5件，由此估计这一批次产品中的次品件数是（　　）

A、5 B、100 C、500 D、10000

查看试题解析
5. 如图，直线l₁∥l₂∥l₃ ，直线AC分别交l₁ ， l₂ ， l₃于点A，B，C，直线DF分别交l₁ ， l₂ ， l₃于点D，E，F，AC与DF相交于点G，且AG=2，GB=1，BC=5，则 $\frac{D E}{E F}$ 的值为（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
6. 与无理数 $\sqrt{31}$ 最接近的整数是（　　）

A、4 B、5 C、6 D、7

查看试题解析
7. 如图，△ABC中，AB=5，BC=3，AC=4，以点C为圆心的圆与AB相切，则⊙C的半径为（）

A、2.3 B、2.4 C、2.5 D、2.6

查看试题解析
8. 一元一次不等式2（x+1）≥4的解在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
9. 数学活动课上，四位同学围绕作图问题：“如图，已知直线l和l外一点P，用直尺和圆规作直线PQ，使PQ⊥l于点Q．”分别作出了下列四个图形．其中作法错误的是（）

A、 B、 C、 D、

查看试题解析
10.
如图，抛物线y=﹣x²+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D，下列四个命题：

①当x＞0时，y＞0；
②若a=﹣1，则b=4；
③抛物线上有两点P（x₁ ， y₁）和Q（x₂ ， y₂），若x₁＜1＜x₂ ，且x₁+x₂＞2，则y₁＞y₂；
④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为6 $\sqrt{2}$ ．
其中真命题的序号是（）

A、① B、② C、③ D、④

查看试题解析

二、填空题

11. 因式分解：ab﹣a= ．

查看试题解析
12. 把一枚均匀的硬币连续抛掷两次，两次正面朝上的概率是．

查看试题解析
13. 一张三角形纸片ABC，AB=AC=5，折叠该纸片使点A落在BC的中点上，折痕经过AC上的点E，则AE的长为．

查看试题解析
14.
如图，多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形，它的面积S可用公式S=a+ $\frac{1}{2}$ b﹣1（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克定理”．现用一张方格纸共有200个格点，画有一个格点多边形，它的面积S=40．

(1)、这个格点多边形边界上的格点数b=（用含a的代数式表示）．

(2)、设该格点多边形外的格点数为c，则c﹣a= ．

查看试题解析
15. 如图，在直角坐标系xOy中，已知点A（0，1），点P在线段OA上，以AP为半径的⊙P周长为1，点M从A开始沿⊙P按逆时针方向转动，射线AM交x轴于点N（n，0）．设点M转过的路程为m（0＜m＜1），随着点M的转动，当m从 $\frac{1}{3}$ 变化到 $\frac{2}{3}$ 时，点N相应移动的路经长为．

查看试题解析

三、解答题

16. 计算下列各题.

(1)、计算：|﹣5|+ $\sqrt{4}$ ×2^﹣¹；

(2)、化简：a（2﹣a）+（a+1）（a﹣1）．

查看试题解析
17. 小明解方程 $\frac{1}{x}$ ﹣ $\frac{x - 2}{x}$ =1的过程如图．请指出他解答过程中的错误，并写出正确的解答过程．

查看试题解析
18. 如图，正方形ABCD中，点E，F分别在边AB，BC上，AF=DE，AF和DE相交于点G，

(1)、观察图形，写出图中所有与∠AED相等的角．

(2)、选择图中与∠AED相等的任意一个角，并加以证明．

查看试题解析
19. 舟山市2010﹣2014年社会消费品零售总额及增速统计图如图：
请根据图中信息，解答下列问题：

(1)、求舟山市2010﹣2014年社会消费品零售总额增速这组数据的中位数．

(2)、求舟山市2010﹣2014年社会消费品零售总额这组数据的平均数．

(3)、用适当的方法预测舟山市2015年社会消费品零售总额（只要求列式说明，不必计算出结果）．

查看试题解析
20. 如图，直线y=2x与反比例函数y= $\frac{k}{x}$ （k≠0，x＞0）的图象交于点A（1，a），B是反比例函数图象上一点，直线OB与x轴的夹角为α，tanα= $\frac{1}{2}$ ．

(1)、求k的值．

(2)、求点B的坐标．

(3)、设点P（m，0），使△PAB的面积为2，求m的值．

查看试题解析
21. 小红将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在水平线的夹角为120°，感觉最舒适（如图1），侧面示意图为图2．使用时为了散热，她在底板下垫入散热架ACO′后，电脑转到AO′B′位置（如图3），侧面示意图为图4．已知OA=OB=24cm，O′C⊥OA于点C，O′C=12cm．

(1)、求∠CAO′的度数．

(2)、显示屏的顶部B′比原来升高了多少？

(3)、如图4，垫入散热架后，要使显示屏O′B与水平线的夹角仍保持120°，则显示屏O′B′应绕点O′按顺时针方向旋转多少度？

查看试题解析
22. 某企业接到一批粽子生产任务，按要求在15天内完成，约定这批粽子的出厂价为每只6元，为按时完成任务，该企业招收了新工人，设新工人李明第x天生产的粽子数量为y只，y与x满足下列关系式：
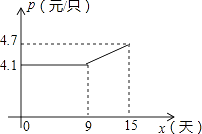y= ${\begin{matrix} 54 x (0 \leq x \leq 5) \\ 30 x + 12 (5 < x \leq 15) \end{matrix}$ ．

(1)、李明第几天生产的粽子数量为420只？

(2)、如图，设第x天每只粽子的成本是p元，p与x之间的关系可用图中的函数图象来刻画．若李明第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大，最大利润是多少元？（利润=出厂价﹣成本）

(3)、设（2）小题中第m天利润达到最大值，若要使第（m+1）天的利润比第m天的利润至少多48元，则第（m+1）天每只粽子至少应提价几元？

查看试题解析
23.
类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

(1)、概念理解：
如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．

(2)、问题探究：
①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由．
②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′，小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离（即线段BB′的长）？

(3)、拓展应用：
如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC，BD为对角线，AC= $\sqrt{2}$ AB，试探究BC，CD，BD的数量关系．

查看试题解析