2015年浙江省义乌市中考数学试卷

试卷更新日期：2017-04-24 类型：中考真卷

进入出卷网下载

一、单项选择题

1. 计算（﹣1）×3的结果是（）

A、﹣3 B、﹣2 C、2 D、3

查看试题解析
2. 据报道，2015年第一季度，义乌电商实现交易额约26 000 000 000元，同比增长22%，将26 000 000 000用科学记数法表示为（　）

A、2.6×10¹⁰ B、2.6×10¹¹ C、26×10¹⁰ D、0.26×10¹¹

查看试题解析
3. 有6个相同的立方体搭成的几何体如图所示，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 下面是一位同学做的四道题：①2a+3b=5ab；②（3a³）²=6a⁶；③a⁶÷a²=a³；④a²•a³=a⁵ ，其中做对的一道题的序号是（　　）

A、① B、② C、③ D、④

查看试题解析
5. 在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球，从中任意摸出一个球，则摸出白球的概率是（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{5}$ C、 $\frac{1}{2}$ D、 $\frac{3}{5}$

查看试题解析
6. 化简 $\frac{x^{2}}{x - 1} + \frac{1}{1 - x}$ 的结果是（）

A、x+1 B、 $\frac{1}{x + 1}$ C、x﹣1 D、 $\frac{x}{x - 1}$

查看试题解析
7. 如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
8. 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B=135°，则 $\hat{A C}$ 的长（）

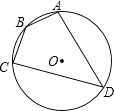A、2π B、π C、 $\frac{π}{2}$ D、 $\frac{π}{3}$

查看试题解析
9. 如果一种变换是将抛物线向右平移2个单位或向上平移1个单位，我们把这种变换称为抛物线的简单变换．已知抛物线经过两次简单变换后的一条抛物线是y=x²+1，则原抛物线的解析式不可能的是（　　）

A、y=x²﹣1 B、y=x²+6x+5 C、y=x²+4x+4 D、y=x²+8x+17

查看试题解析
10.
挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走．如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走（）

A、②号棒 B、⑦号棒 C、⑧号棒 D、⑩号棒

查看试题解析

二、填空题

11. 分解因式：x²﹣4= ．

查看试题解析
12. 如图，已知点A（0，1），B（0，﹣1），以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则∠BAC等于度．

查看试题解析
13. 由于木质衣架没有柔性，在挂置衣服的时候不太方便操作．小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可．如图1，衣架杆OA=OB=18cm，若衣架收拢时，∠AOB=60°，如图2，则此时A，B两点之间的距离是 cm．

查看试题解析
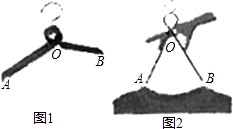14. 在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB．若PB=4，则PA的长为．

查看试题解析
15. 在平面直角坐标系的第一象限内，边长为1的正方形ABCD的边均平行于坐标轴，A点的坐标为（a，a）．如图，若曲线 $y = \frac{3}{x} (x > 0)$ 与此正方形的边有交点，则a的取值范围是．

查看试题解析
16. 实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1：2：1，用两个相同的管子在容器的5cm高度处连通（即管子底离容器底5cm），现三个容器中，只有甲中有水，水位高1cm，如图所示．若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升 $\frac{5}{6}$ cm．

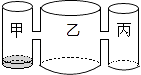(1)、开始注水1分钟，丙的水位上升 cm．

(2)、开始注入分钟的水量后，乙的水位比甲高0.5cm．

查看试题解析

三、解答题

17. 计算下列各题

(1)、 $2 \cos 45^{\circ} - {(π + 1)}^{0} + \sqrt{\frac{1}{4}} + {(\frac{1}{2})}^{- 1}$ ；

(2)、解不等式：3x﹣5≤2（x+2）

查看试题解析
18.
小敏上午8：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中．小敏离家的路程y（米）和所经过的时间x（分）之间的函数图象如图所示．请根据图象回答下列问题：

(1)、小敏去超市途中的速度是多少？在超市逗留了多少时间？

(2)、小敏几点几分返回到家？

查看试题解析
19. 为了解某种电动汽车的性能，对这种电动汽车进行了抽检，将一次充电后行驶的里程数分为A，B，C，D四个等级，其中相应等级的里程依次为200千米，210千米，220千米，230千米，获得如下不完整的统计图．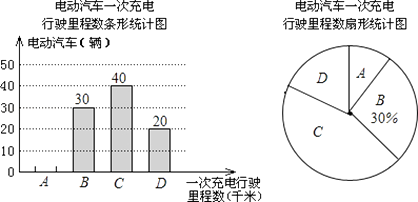
根据以上信息，解答下列问题：

(1)、问这次被抽检的电动汽车共有几辆？并补全条形统计图；

(2)、估计这种电动汽车一次充电后行驶的平均里程数为多少千米？

查看试题解析
20.
如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走6m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．

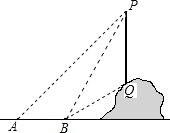(1)、求∠BPQ的度数；

(2)、求该电线杆PQ的高度（结果精确到1m）．
备用数据： $\sqrt{3} \approx 1.7$ ， $\sqrt{2} \approx 1.4$ ．

查看试题解析
21. 如果抛物线y=ax²+bx+c过定点M（1，1），则称此抛物线为定点抛物线．

(1)、张老师在投影屏幕上出示了一个题目：请你写出一条定点抛物线的一个解析式．小敏写出了一个答案：y=2x²+3x﹣4，请你写出一个不同于小敏的答案；

(2)、张老师又在投影屏幕上出示了一个思考题：已知定点抛物线y=﹣x²+2bx+c+1，求该抛物线顶点纵坐标的值最小时的解析式，请你解答．

查看试题解析
22. 某校规划在一块长AD为18m，宽AB为13m的长方形场地ABCD上，设计分别与AD，AB平行的横向通道和纵向通道，其余部分铺上草皮．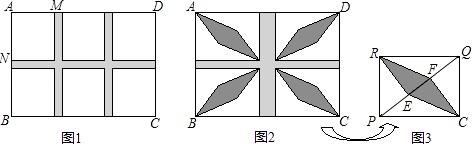

(1)、如图1，若设计三条通道，一条横向，两条纵向，且它们的宽度相等，其余六块草坪相同，其中一块草坪两边之比AM：AN=8：9，问通道的宽是多少？

(2)、为了建造花坛，要修改（1）中的方案，如图2，将三条通道改为两条通道，纵向的宽度改为横向宽度的2倍，其余四块草坪相同，且每一块草坪均有一边长为8m，这样能在这些草坪建造花坛．如图3，在草坪RPCQ中，已知RE⊥PQ于点E，CF⊥PQ于点F，求花坛RECF的面积．

查看试题解析
23. 正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A按顺时针方向旋转，记旋转角∠DAG=α，其中0°≤α≤180°，连结DF，BF，如图．

(1)、若α=0°，则DF=BF，请加以证明；

(2)、试画一个图形（即反例），说明（1）中命题的逆命题是假命题；

(3)、对于（1）中命题的逆命题，如果能补充一个条件后能使该逆命题为真命题，请直接写出你认为需要补充的一个条件，不必说明理由．

查看试题解析
24.
在平面直角坐标系中，O为原点，四边形OABC的顶点A在x轴的正半轴上，OA=4，OC=2，点P，点Q分别是边BC，边AB上的点，连结AC，PQ，点B₁是点B关于PQ的对称点．

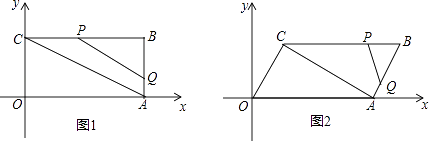(1)、若四边形OABC为矩形，如图1，
①求点B的坐标；
②若BQ：BP=1：2，且点B₁落在OA上，求点B₁的坐标；

(2)、若四边形OABC为平行四边形，如图2，且OC⊥AC，过点B₁作B₁F∥x轴，与对角线AC、边OC分别交于点E、点F．若B₁E：B₁F=1：3，点B₁的横坐标为m，求点B₁的纵坐标，并直接写出m的取值范围．

查看试题解析