2015年浙江省台州市中考数学试卷
试卷更新日期：2017-04-24 类型：中考真卷
一、选择题
-
1. 单项式2a的系数是（ ）A、2 B、2a C、1 D、a2. 下列四个几何体中，左视图为圆的是（ ）A、
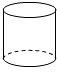B、
C、
D、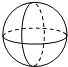
3. 在下列调查中，适宜采用全面调查的是（ ）A、了解我省中学生的视力情况 B、了解九（1）班学生校服的尺码情况 C、检测一批电灯泡的使用寿命 D、调查台州《600全民新闻》栏目的收视率4. 若反比例函数y=的图象经过点（2，﹣1），则该反比例函数的图象在（ ）A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限5. 若一组数据3，x，4，5，6的众数为6，则这组数据的中位数为（ ）A、3 B、4 C、5 D、66. 把多项式2x2﹣8分解因式，结果正确的是（ ）A、2（x2﹣8） B、2（x﹣2）2 C、2（x+2）（x﹣2） D、2x（x﹣）7. 设二次函数y=（x﹣3）2﹣4图象的对称轴为直线l，若点M在直线l上，则点M的坐标可能是（ ）A、（1，0） B、（3，0） C、（﹣3，0） D、（0，﹣4）8. 如果将长为6cm，宽为5cm的长方形纸片折叠一次，那么这条折痕的长不可能是（ ）
A、8cm B、5cm C、5.5cm D、1cm9.如图，在菱形ABCD中，AB=8，点E，F分别在AB，AD上，且AE=AF，过点E作EG∥AD交CD于点G，过点F作FH∥AB交BC于点H，EG与FH交于点O．当四边形AEOF与四边形CGOH的周长之差为12时，AE的值为（ ）
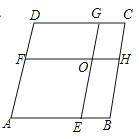A、6.5 B、6 C、5.5 D、510. 某班有20位同学参加围棋、象棋比赛，甲说：“只参加一项的人数大于14人．”乙说：“两项都参加的人数小于5．”对于甲、乙两人的说法，有下列四个命题，其中真命题的是（ ）A、若甲对，则乙对 B、若乙对，则甲对 C、若乙错，则甲错 D、若甲错，则乙对二、填空题
-
11. 不等式2x﹣4≥0的解集是 ．12. 有四张质地、大小、反面完全相同的不透明卡片，正面分别写着数字1，2，3，4，现把它们的正面向下，随机摆放在桌面上，从中任意抽出一张，则抽出的数字是奇数的概率是 ．13. 如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，DC=3，则点D到AB的距离是 ．
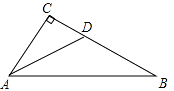14. 如图，这是台州市地图的一部分，分别以正东、正北方向为x轴、y轴的正方向建立直角坐标系，规定一个单位长度表示1km，甲、乙两人对着地图如下描述路桥区A处的位置．
则椒江区B处的坐标是 ．
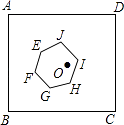
15. 关于x的方程mx2+x﹣m+1=0，有以下三个结论：①当m=0时，方程只有一个实数解；②当m≠0时，方程有两个不等的实数解；③无论m取何值，方程都有一个负数解，其中正确的是（填序号）．16.如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个正六边形的边长最大时，AE的最小值为 ．
三、解答题
-
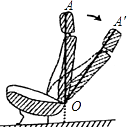
17. 计算：6÷（﹣3）+|﹣1|﹣20150 ．18. 先化简，再求值： ﹣ ，其中a= ﹣1．19. 如图，这是一把可调节座椅的侧面示意图，已知头枕上的点A到调节器点O处的距离为80cm，AO与地面垂直，现调整靠背，把OA绕点O旋转35°到OA′处，求调整后点A′比调整前点A的高度降低了多少厘米（结果取整数）？
（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
20. 图1中的摩天轮可抽象成一个圆，圆上一点离地面的高度y（m）与旋转时间x（min）之间的关系如图2所示．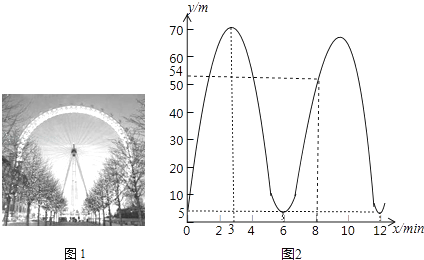
(1)、根据图2填表：x（min）
0
3
6
8
12
…
y（m）
…
(2)、变量y是x的函数吗？为什么？(3)、根据图中的信息，请写出摩天轮的直径．21. 某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分布直方图和扇形统计图．根据图中提供的信息，解答下列问题：
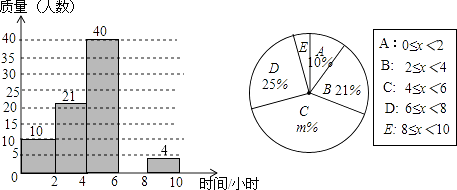(1)、补全频数分布直方图；(2)、求扇形统计图中m的值和“E”组对应的圆心角度数；(3)、请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数．22. 如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC．
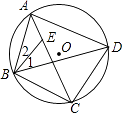(1)、若∠CBD=39°，求∠BAD的度数；(2)、求证：∠1=∠2．23.如图，在多边形ABCDE中，∠A=∠AED=∠D=90°，AB=5，AE=2，ED=3，过点E作EF∥CB交AB于点F，FB=1，过AE上的点P作PQ∥AB交线段EF于点O，交折线BCD于点Q，设AP=x，PO•OQ=y．
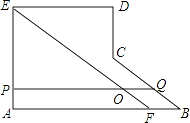(1)、①延长BC交ED于点M，则MD= ， DC=；
(2)、求y关于x的函数解析式；
(3)、当a≤x≤ （a＞0）时，9a≤y≤6b，求a，b的值；
(4)、当1≤y≤3时，请直接写出x的取值范围．
24.定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．
(1)、已知点M，N是线段AB的勾股分割点，若AM=2，MN=3，求BN的长；(2)、如图2，在△ABC中，FG是中位线，点D，E是线段BC的勾股分割点，且EC＞DE≥BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点；(3)、已知点C是线段AB上的一定点，其位置如图3所示，请在BC上画一点D，使点C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画一种情形即可）；(4)、如图4，已知点M，N是线段AB的勾股分割点，MN＞AM≥BN，△AMC，△MND和△NBE均为等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，试探究S△AMF ， S△BEN和S四边形MNHG的数量关系，并说明理由．