2015年浙江省丽水市中考数学试卷

试卷更新日期：2017-04-24 类型：中考真卷

进入出卷网下载

一、选择题

1. 在数﹣3，﹣2，0，3中，大小在﹣1和2之间的数是（）

A、﹣3 B、﹣2 C、0 D、3

查看试题解析
2. 计算（a²）³的正确结果是（　　）

A、3a² B、a⁶ C、a⁵ D、6a

查看试题解析
3. 由4个相同的小立方体搭成的几何体如图所示，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 分式﹣ $\frac{1}{1 - x}$ 可变形为（）

A、﹣ $\frac{1}{x - 1}$ B、 $\frac{1}{1 + x}$ C、﹣ $\frac{1}{1 + x}$ D、 $\frac{1}{x - 1}$

查看试题解析
5. 一个多边形的每个内角均为120°，则这个多边形是（　　）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
6. 如图，数轴上所表示关于x的不等式组的解集是（）

A、x≥2 B、x＞2 C、x＞﹣1 D、﹣1＜x≤2

查看试题解析
7. 某小组7位学生的中考体育测试成绩（满分30分）依次为27，30，29，27，30，28，30．则这组数据的众数与中位数分别是（　　）

A、30，27 B、30，29 C、29，30 D、30，28

查看试题解析
8. 如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的是（）

A、 $\frac{B D}{B C}$ B、 $\frac{B C}{A B}$ C、 $\frac{A D}{A C}$ D、 $\frac{C D}{A C}$

查看试题解析
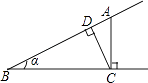9. 在平面直角坐标系中，过点（﹣2，3）的直线l经过一、二、三象限，若点（0，a），（﹣1，b），（c，﹣1）都在直线l上，则下列判断正确的是（　　）

A、a＜b B、a＜3 C、b＜3 D、c＜﹣2

查看试题解析
10. 如图，在方格纸中，线段a，b，c，d的端点在格点上，通过平移其中两条线段，使得和第三条线段首尾相接组成三角形，则能组成三角形的不同平移方法有（）

A、3种 B、6种 C、8种 D、12种

查看试题解析

二、填空题

11. 分解因式：9﹣x²= ．

查看试题解析
12. 有6张卡片，每张卡片上分别写有不同的从1到6的一个自然数．从中任意抽出一张卡片，卡片上的数是3的倍数的概率是．

查看试题解析
13. 如图，圆心角∠AOB=20°，将 $\hat{A B}$ 旋转n°得到 $\hat{C D}$ ，则 $\hat{C D}$ 的度数是度．

查看试题解析
14. 解一元二次方程x²+2x﹣3=0时，可转化为解两个一元一次方程，请写出其中的一个一元一次方程．

查看试题解析
15. 如图，四边形ABCD与四边形AECF都是菱形，点E、F在BD上．已知∠BAD=120°，∠EAF=30°，则 $\frac{A B}{A E}$ = ．

查看试题解析
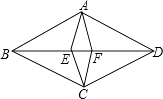16.
如图，反比例函数y= $\frac{k}{x}$ 的图象经过点（﹣1，﹣2 $\sqrt{2}$ ），点A是该图象第一象限分支上的动点，连结AO并延长交另一分支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第四象限，AC与x轴交于点P，连结BP．

(1)、k的值为．

(2)、在点A运动过程中，当BP平分∠ABC时，点C的坐标是．

查看试题解析

三、解答题

17. 计算：|﹣4|+（﹣ $\sqrt{2}$ ）⁰﹣（ $\frac{1}{2}$ ）^﹣¹ ．

查看试题解析
18. 先化简，再求值：a（a﹣3）+（1﹣a）（1+a），其中a= $\frac{\sqrt{3}}{3}$ ．

查看试题解析
19. 如图，已知△ABC，∠C=90°，AC＜BC．D为BC上一点，且到A，B两点的距离相等．

(1)、用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；

(2)、连结AD，若∠B=37°，求∠CAD的度数．

查看试题解析
20. 某运动品牌店对第一季度A、B两款运动鞋的销售情况进行统计．两款运动鞋的销售量及总销售额如图所示：

(1)、一月份B款运动鞋的销售量是A款的 $\frac{4}{5}$ ，则一月份B款运动鞋销售了多少双？

(2)、第一节度这两款运动鞋的销售单价保持不变，求三月份的总销售额（销售额=销售单价×销售量）；

(3)、综合第一季度的销售情况，请你对这两款运动鞋的进货、销售等方面提出一条建议．

查看试题解析
21. 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作⊙O的切线DF，交AC于点F．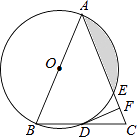

(1)、求证：DF⊥AC；

(2)、若⊙O的半径为4，∠CDF=22.5°，求阴影部分的面积．

查看试题解析
22. 甲、乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走．设甲、乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象的一部分如图所示．

(1)、求甲行走的速度；

(2)、在坐标系中，补画s关于t的函数图象的其余部分；

(3)、问甲、乙两人何时相距360米？

查看试题解析
23. 如图，在矩形ABCD中，E为CD的中点，F为BE上的一点，连结CF并延长交AB于点M，MN⊥CM交射线AD于点N．

(1)、当F为BE中点时，求证：AM=CE；

(2)、若 $\frac{A B}{B C} = \frac{E F}{B F}$ =2，求 $\frac{A N}{N D}$ 的值；

(3)、若 $\frac{A B}{B C} = \frac{E F}{B F}$ =n，当n为何值时，MN∥BE？

查看试题解析
24.
某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，假设每次发出的乒乓球的运动路线固定不变，且落在中线上．在乒乓球运行时，设乒乓球与端点A的水平距离为x（米），与桌面的高度为y（米），运行时间为t（秒），经多次测试后，得到如下部分数据：
t（秒）
0
0.16
0.2
0.4
0.6
0.64
0.8
6
X（米）
0
0.4
0.5
1
1.5
1.6
2
…
y（米）
0.25
0.378
0.4
0.45
0.4
0.378
0.25
…

(1)、当t为何值时，乒乓球达到最大高度？

(2)、乒乓球落在桌面时，与端点A的水平距离是多少？

(3)、乒乓球落在桌面上弹起后，y与x满足y=a（x﹣3）²+k．
①用含a的代数式表示k；
②球网高度为0.14米，球桌长（1.4×2）米．若球弹起后，恰好有唯一的击球点，可以将球沿直线扣杀到点A，求a的值．

查看试题解析

t（秒）	0	0.16	0.2	0.4	0.6	0.64	0.8	6
X（米）	0	0.4	0.5	1	1.5	1.6	2	…
y（米）	0.25	0.378	0.4	0.45	0.4	0.378	0.25	…