2015年浙江省杭州市中考数学试卷
试卷更新日期：2017-04-24 类型：中考真卷
一、仔细选一选
-
1. 统计显示，2013年底杭州市各类高中在校学生人数大约是11.4万人，将11.4万用科学记数法表示应为（ ）A、11.4×102 B、1.14×103 C、1.14×104 D、1.14×1052. 下列计算正确的是（ ）A、23+26=29 B、23﹣24=2﹣1 C、23×23=29 D、24÷22=223. 下列图形是中心对称图形的是（ ）
A、
B、
C、
D、
4. 下列各式的变形中，正确的是（ ）A、（﹣x﹣y）（﹣x+y）=x2﹣y2 B、 ﹣x= C、x2﹣4x+3=（x﹣2）2+1 D、x÷（x2+x）= +15. 圆内接四边形ABCD中，已知∠A=70°，则∠C=（ ）A、20° B、30° C、70° D、110°6. 若k＜＜k+1（k是整数），则k=（ ）A、6 B、7 C、8 D、97. 某村原有林地108公顷，旱地54公顷，为保护环境，需把一部分旱地改造为林地，使旱地面积占林地面积的20%．设把x公顷旱地改为林地，则可列方程（ ）A、54﹣x=20%×108 B、54﹣x=20%（108+x） C、54+x=20%×162 D、108﹣x=20%（54+x）8. 如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图（当AQI不大于100时称空气质量为“优良”）．由图可得下列说法：①18日的PM2.5浓度最低；②这六天中PM2.5浓度的中位数是112μg/m3；③这六天中有4天空气质量为“优良”；④空气质量指数AQI与PM2.5浓度有关．其中正确的是（ ）
A、①②③ B、①②④ C、①③④ D、②③④9. 如图，已知点A，B，C，D，E，F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段．在连接两点所得的所有线段中任取一条线段，取到长度为 的线段的概率为（ ）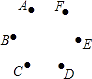
A、 B、 C、 D、10. 设二次函数y1=a（x﹣x1）（x﹣x2）（a≠0，x1≠x2）的图象与一次函数y2=dx+e（d≠0）的图象交于点（x1 ， 0），若函数y=y1+y2的图象与x轴仅有一个交点，则（ ）A、a（x1﹣x2）=d B、a（x2﹣x1）=d C、a（x1﹣x2）2=d D、a（x1+x2）2=d二、认真填一填
-
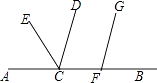
11. 数据1，2，3，5，5的众数是 ， 平均数是 ．12. 分解因式：m3n﹣4mn= ．13. 函数y=x2+2x+1，当y=0时，x=；当1＜x＜2时，y随x的增大而（填写“增大”或“减小”）．14. 如图，点A，C，F，B在同一直线上，CD平分∠ECB，FG∥CD．若∠ECA为α度，则∠GFB为度（用关于α的代数式表示）．
15. 在平面直角坐标系中，O为坐标原点，设点P（1，t）在反比例函数y= 的图象上，过点P作直线l与x轴平行，点Q在直线l上，满足QP=OP．若反比例函数y= 的图象经过点Q，则k= ．16. 如图，在四边形纸片ABCD中，AB=BC，AD=CD，∠A=∠C=90°，∠B=150°．将纸片先沿直线BD对折，再将对折后的图形沿从一个顶点出发的直线裁剪，剪开后的图形打开铺平．若铺平后的图形中有一个是面积为2的平行四边形，则CD= ．
三、全面答一答
-
17.
杭州市推行垃圾分类已经多年，但在剩余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾．如图是杭州某一天收到的厨余垃圾的统计图．
(1)、试求出m的值；(2)、杭州市某天收到厨余垃圾约200吨，请计算其中混杂着的玻璃类垃圾的吨数．18. 如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M，N分别在AB，AC边上，AM=2MB，AN=2NC．求证：DM=DN．
19. 如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′•OP=r2 ， 则称点P′是点P关于⊙O的“反演点”．如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．
20. 设函数y=（x﹣1）[（k﹣1）x+（k﹣3）]（k是常数）．
(1)、当k取1和2时的函数y1和y2的图象如图所示，请你在同一直角坐标系中画出当k取0时的函数的图象；(2)、根据图象，写出你发现的一条结论；(3)、将函数y2的图象向左平移4个单位，再向下平移2个单位，得到的函数y3的图象，求函数y3的最小值．21. “综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度．(1)、用记号（a，b，c）（a≤b≤c）表示一个满足条件的三角形，如（2，3，3）表示边长分别为2，3，3个单位长度的一个三角形．请列举出所有满足条件的三角形．(2)、用直尺和圆规作出三边满足a＜b＜c的三角形（用给定的单位长度，不写作法，保留作图痕迹）．22. 如图，在△ABC中（BC＞AC），∠ACB=90°，点D在AB边上，DE⊥AC于点E．
(1)、若 = ，AE=2，求EC的长；(2)、设点F在线段EC上，点G在射线CB上，以F，C，G为顶点的三角形与△EDC有一个锐角相等，FG交CD于点P．问：线段CP可能是△CFG的高线还是中线？或两者都有可能？请说明理由．23. 方成同学看到一则材料：甲开汽车，乙骑自行车从M地出发沿一条公路匀速前往N地．设乙行驶的时间为t（h），甲乙两人之间的距离为y（km），y与t的函数关系如图1所示．方成思考后发现了如图1的部分正确信息：乙先出发1h；甲出发0.5小时与乙相遇．
请你帮助方成同学解决以下问题：
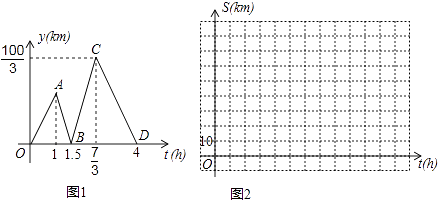(1)、分别求出线段BC，CD所在直线的函数表达式；(2)、当20＜y＜30时，求t的取值范围；(3)、分别求出甲，乙行驶的路程S甲 ， S乙与时间t的函数表达式，并在图2所给的直角坐标系中分别画出它们的图象；(4)、丙骑摩托车与乙同时出发，从N地沿同一公路匀速前往M地，若丙经过 h与乙相遇，问丙出发后多少时间与甲相遇？