2014年浙江省绍兴市中考数学试卷

试卷更新日期：2017-04-24 类型：中考真卷

进入出卷网下载

一、选择题

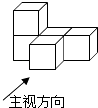
1. 比较﹣3，1，﹣2的大小，下列判断正确的是（）

A、﹣3＜﹣2＜1 B、﹣2＜﹣3＜1 C、1＜﹣2＜﹣3 D、1＜﹣3＜﹣2

查看试题解析
2. 计算（ab）²的结果是（）

A、2ab B、a²b C、a²b² D、ab²

查看试题解析
3. 太阳的温度很高，其表面温度大概有6 000℃，而太阳中心的温度达到了19 200 000℃，用科学记数法可将19 200 000表示为（）

A、1.92×10⁶ B、1.92×10⁷ C、1.92×10⁸ D、1.92×10⁹

查看试题解析
4. 由5个相同的立方体搭成的几何体如图所示，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 一个不透明的袋子中有2个白球，3个黄球和1个红球，这些球除颜色不同外其他完全相同，则从袋子中随机摸出一个球是白球的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 不等式3x+2＞﹣1的解集是（）

A、x＞﹣ $\frac{1}{3}$ B、x＜﹣ $\frac{1}{3}$ C、x＞﹣1 D、x＜﹣1

查看试题解析
7. 如图，圆锥的侧面展开图是半径为3，圆心角为90°的扇形，则该圆锥的底面周长为（）

A、 $\frac{3}{4}$ π B、 $\frac{3}{2}$ π C、 $\frac{3}{4}$ D、 $\frac{3}{2}$

查看试题解析
8. 如图1，天平呈平衡状态，其中左侧秤盘中有一袋玻璃球，右侧秤盘中也有一袋玻璃球，还有2个各20克的砝码．现将左侧袋中一颗玻璃球移至右侧秤盘，并拿走右侧秤盘的1个砝码后，天平仍呈平衡状态，如图2，则被移动的玻璃球的质量为（）

A、10克 B、15克 C、20克 D、25克

查看试题解析
9. 将一张正方形纸片，按如图步骤①，②，沿虚线对折两次，然后沿③中的虚线剪去一个角，展开铺平后的图形是（）

A、 B、 C、 D、

查看试题解析
10. 如图，汽车在东西向的公路l上行驶，途中A，B，C，D四个十字路口都有红绿灯．AB之间的距离为800米，BC为1000米，CD为1400米，且l上各路口的红绿灯设置为：同时亮红灯或同时亮绿灯，每次红（绿）灯亮的时间相同，红灯亮的时间与绿灯亮的时间也相同．若绿灯刚亮时，甲汽车从A路口以每小时30千米的速度沿l向东行驶，同时乙汽车从D路口以相同的速度沿l向西行驶，这两辆汽车通过四个路口时都没有遇到红灯，则每次绿灯亮的时间可能设置为（）

A、50秒 B、45秒 C、40秒 D、35秒

查看试题解析

二、填空题

11. 分解因式：a²﹣a= ．

查看试题解析
12. 把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为．

查看试题解析
13. 如图的一座拱桥，当水面宽AB为12m时，桥洞顶部离水面4m，已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点A为坐标原点时的抛物线解析式是y=﹣ $\frac{1}{9}$ （x﹣6）²+4，则选取点B为坐标原点时的抛物线解析式是．

查看试题解析
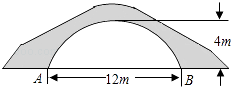14. 用直尺和圆规作△ABC，使BC=a，AC=b，∠B=35°，若这样的三角形只能作一个，则a，b间满足的关系式是．

查看试题解析
15. 如图，边长为n的正方形OABC的边OA，OC在坐标轴上，点A₁ ， A₂ ， …，A_n_﹣₁为OA的n等分点，点B₁ ， B₂ ， …，B_n_﹣₁为CB的n等分点，连结A₁B₁ ， A₂B₂ ， …，A_n_﹣₁B_n_﹣₁ ，分别交曲线y= $\frac{n - 2}{x}$ （x＞0）于点C₁ ， C₂ ， …，C_n_﹣₁ ．若C₁₅B₁₅=16C₁₅A₁₅ ，则n的值为．（n为正整数）

查看试题解析
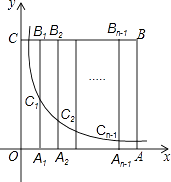16. 把标准纸一次又一次对开，可以得到均相似的“开纸”．现在我们在长为2 $\sqrt{2}$ 、宽为1的矩形纸片中，画两个小矩形，使这两个小矩形的每条边都与原矩形纸的边平行，或小矩形的边在原矩形的边上，且每个小矩形均与原矩形纸相似，然后将它们剪下，则所剪得的两个小矩形纸片周长之和的最大值是．

查看试题解析

三、解答题

17. 计算下列各题

(1)、计算： ${(\frac{1}{2})}^{- 1}$ ﹣4sin45°﹣ ${(1 - \sqrt{2})}^{0}$ + $\sqrt{8}$ ．

(2)、先化简，再求值：a（a﹣3b）+（a+b）²﹣a（a﹣b），其中a=1，b=﹣ $\frac{1}{2}$ ．

查看试题解析
18. 已知甲、乙两地相距90km，A，B两人沿同一公路从甲地出发到乙地，A骑摩托车，B骑电动车，图中DE，OC分别表示A，B离开甲地的路程s（km）与时间t（h）的函数关系的图象，根据图象解答下列问题．

(1)、A比B后出发几个小时？B的速度是多少？

(2)、在B出发后几小时，两人相遇？

查看试题解析
19.
为了解某校七，八年级学生的睡眠情况，随机抽取了该校七，八年级部分学生进行调查，已知抽取七年级与八年级的学生人数相同，利用抽样所得的数据绘制如下统计图表．

睡眠情况分组表（单位：时）
组别
睡眠时间x
A
x≤7.5
B
7.5≤x≤8.5
C
8.5≤x≤9.5
D
9.5≤x≤10.5
E
x≥10.5
根据图表提供的信息，回答下列问题：

(1)、求统计图中的a；

(2)、抽取的样本中，八年级学生睡眠时间在C组的有多少人？

(3)、已知该校七年级学生有755人，八年级学生有785人，如果睡眠时间x（时）满足：7.5≤x≤9.5，称睡眠时间合格，试估计该校七、八年级学生中睡眠时间合格的共有多少人？

查看试题解析
20. 课本中有一道作业题：
有一块三角形余料ABC，它的边BC=120mm，高AD=80mm．要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．问加工成的正方形零件的边长是多少mm？
小颖解得此题的答案为48mm，小颖善于反思，她又提出了如下的问题．

(1)、如果原题中要加工的零件是一个矩形，且此矩形是由两个并排放置的正方形所组成，如图1，此时，这个矩形零件的两条边长又分别为多少mm？请你计算．

(2)、如果原题中所要加工的零件只是一个矩形，如图2，这样，此矩形零件的两条边长就不能确定，但这个矩形面积有最大值，求达到这个最大值时矩形零件的两条边长．

查看试题解析
21.
九（1）班同学在上学期的社会实践活动中，对学校旁边的山坡护墙和旗杆进行了测量．

(1)、如图1，第一小组用一根木条CD斜靠在护墙上，使得DB与CB的长度相等，如果测量得到∠CDB=38°，求护墙与地面的倾斜角α的度数．

(2)、如图2，第二小组用皮尺量的EF为16米（E为护墙上的端点），EF的中点离地面FB的高度为1.9米，请你求出E点离地面FB的高度．

(3)、如图3，第三小组利用第一、第二小组的结果，来测量护墙上旗杆的高度，在点P测得旗杆顶端A的仰角为45°，向前走4米到达Q点，测得A的仰角为60°，求旗杆AE的高度（精确到0.1米）．
备用数据：tan60°=1.732，tan30°=0.577， $\sqrt{3}$ =1.732， $\sqrt{2}$ =1.414．

查看试题解析
22. 如果二次函数的二次项系数为l，则此二次函数可表示为y=x²+px+q，我们称[p，q]为此函数的特征数，如函数y=x²+2x+3的特征数是[2，3]．

(1)、若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．

(2)、探究下列问题：
①若一个函数的特征数为[4，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．
②若一个函数的特征数为[2，3]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[3，4]？

查看试题解析
23.

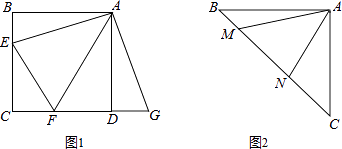(1)、如图1，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连结EF，AG．求证：EF=FG．

(2)、如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长．

查看试题解析
24. 如图，在平面直角坐标系中，直线l平行x轴，交y轴于点A，第一象限内的点B在l上，连结OB，动点P满足∠APQ=90°，PQ交x轴于点C．

(1)、当动点P与点B重合时，若点B的坐标是（2，1），求PA的长．

(2)、当动点P在线段OB的延长线上时，若点A的纵坐标与点B的横坐标相等，求PA：PC的值．

(3)、当动点P在直线OB上时，点D是直线OB与直线CA的交点，点E是直线CP与y轴的交点，若∠ACE=∠AEC，PD=2OD，求PA：PC的值．

查看试题解析

组别	睡眠时间x
A	x≤7.5
B	7.5≤x≤8.5
C	8.5≤x≤9.5
D	9.5≤x≤10.5
E	x≥10.5